题目内容
设向量 ,
,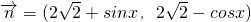 ,若
,若
求:(1)f(x)的单调递增区间
(2)若 ,且f(θ)=1,求
,且f(θ)=1,求 的值.
的值.
解:(1)∵向量 ,
,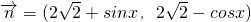 ,
,
∴ =cosx(2
=cosx(2 +sinx)+sinx(2
+sinx)+sinx(2 -cosx)
-cosx)
=2 cosx+cosxsinx+2
cosx+cosxsinx+2 sinx-sinxcosx
sinx-sinxcosx
=2 (cosx+sinx)
(cosx+sinx)
∴ ,
,
∴x+ ∈[2kπ-
∈[2kπ- ,2kπ+
,2kπ+ ]
]
∴单调增区间为
(2)∵ ,
,
∴f(θ)=4sin(θ+ )=1
)=1
∴sin(θ+ )=
)=
∵

∴
∴sin( )=sin[(
)=sin[( )+
)+ ]=sin(
]=sin( )cos
)cos +sin(
+sin( )sin
)sin ,
,
∴ .
.
分析:(1)根据所给的向量的坐标和数量积公式,整理出关于x的关系式,利用辅角公式把三角函数式变化成最简单形式,应用正弦函数的单调性求出函数的单调性.
(2)根据所给的等式,得到角的关系式,根据角的范围利用同角的三角函数关系,得到要用的角的三角函数值,把要求的角的三角函数变化,假期哦的变化时本题的重点.
点评:已知一个角的某一个三角函数值,便可运用基本关系式求出其它三角函数值.在求值中,确定角的终边位置是关键和必要的.有时,由于角的终边位置的不确定,因此解的情况不止一种.
 ,
,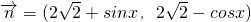 ,
,∴
 =cosx(2
=cosx(2 +sinx)+sinx(2
+sinx)+sinx(2 -cosx)
-cosx)=2
 cosx+cosxsinx+2
cosx+cosxsinx+2 sinx-sinxcosx
sinx-sinxcosx=2
 (cosx+sinx)
(cosx+sinx)∴
 ,
,∴x+
 ∈[2kπ-
∈[2kπ- ,2kπ+
,2kπ+ ]
]∴单调增区间为

(2)∵
 ,
,∴f(θ)=4sin(θ+
 )=1
)=1∴sin(θ+
 )=
)=
∵


∴

∴sin(
 )=sin[(
)=sin[( )+
)+ ]=sin(
]=sin( )cos
)cos +sin(
+sin( )sin
)sin ,
,∴
 .
.分析:(1)根据所给的向量的坐标和数量积公式,整理出关于x的关系式,利用辅角公式把三角函数式变化成最简单形式,应用正弦函数的单调性求出函数的单调性.
(2)根据所给的等式,得到角的关系式,根据角的范围利用同角的三角函数关系,得到要用的角的三角函数值,把要求的角的三角函数变化,假期哦的变化时本题的重点.
点评:已知一个角的某一个三角函数值,便可运用基本关系式求出其它三角函数值.在求值中,确定角的终边位置是关键和必要的.有时,由于角的终边位置的不确定,因此解的情况不止一种.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 =(cosωx-sinωx,-1),
=(cosωx-sinωx,-1), =(2sinωx,-1),其中ω>0,x∈R,已知函数f(x)=
=(2sinωx,-1),其中ω>0,x∈R,已知函数f(x)= •
• 的最小正周期为4π.
的最小正周期为4π. ,求f(x)的值.
,求f(x)的值. 中,角
中,角 为锐角,记角
为锐角,记角 所对的边分别为
所对的边分别为 设向量
设向量
 且
且 与
与 的夹角为
的夹角为
 的值及角
的值及角 ,求
,求 .
. 中,角
中,角 为锐角,记角
为锐角,记角 所对的边分别为
所对的边分别为 ,设向量
,设向量 ,且
,且 的夹角为
的夹角为
 的值及角
的值及角 ,求
,求 .
. ,
, ,若
,若
 ,且f(θ)=1,求
,且f(θ)=1,求 的值.
的值.