题目内容
若函数f(x)=1+2mx+(m2-1)x2是偶函数,则m= .
【答案】分析:根据二次函数f(x)的对称轴为 x=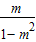 ,函数是偶函数,可得
,函数是偶函数,可得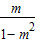 =0,由此解得 m的值.
=0,由此解得 m的值.
解答:解:由于二次函数f(x)=1+2mx+(m2-1)x2的对称轴为 x=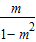 .
.
再由此函数是偶函数,可得函数的图象关于y轴对称,故有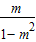 =0,解得 m=0,
=0,解得 m=0,
故答案为 0.
点评:本题主要考查二次函数的性质,函数的奇偶性的性质,属于基础题.
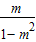 ,函数是偶函数,可得
,函数是偶函数,可得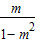 =0,由此解得 m的值.
=0,由此解得 m的值.解答:解:由于二次函数f(x)=1+2mx+(m2-1)x2的对称轴为 x=
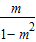 .
.再由此函数是偶函数,可得函数的图象关于y轴对称,故有
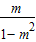 =0,解得 m=0,
=0,解得 m=0,故答案为 0.
点评:本题主要考查二次函数的性质,函数的奇偶性的性质,属于基础题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 设函数f(x)=
设函数f(x)=