题目内容
4.已知数列{an}满足:a1=3,an+1=an2-nan+1.(Ⅰ)求a2,a3,a4的值;
(Ⅱ)猜测an与n+2的关系,并用数学归纳法证明.
分析 (Ⅰ)通过an+1=an2-nan+1、a1=3代入计算即得结论;
(Ⅱ)先证明n=1时不等式成立,再假设n=k时不等式成立,进而论证n=k+1时,不等式依然成立,最终得到不等式an≥n+2恒成立.
解答 解:(Ⅰ)依题意,a2=a12-a1+1=32-3+1=7,
a3=a22-2a2+1=72-2×7+1=36,
a4=a32-3a3+1=362-3×36+1=1189;
(Ⅱ)结论:an≥n+2的关系.
用数学归纳法证明如下:
①当n=1时,a1=3=1+2,不等式成立;
②假设当n=k(k≥2)时不等式成立,即ak≥k+2,
那么ak+1=ak(ak-k)+1
≥(k+2)(k+2-k)+1
=2k+5
≥k+3,
也就是说,当n=k+1时,ak+1≥(k+1)+2;
由①、②可知:对于所有n≥1,有an≥n+2.
点评 本题考查数列的通项,考查数列归纳法,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
19.先后掷骰子两次,落在水平桌面后,记正面朝上的点数分别为x,y,设事件A为“x+y为偶数”,事件B为“x≠y”,则概率P(B|A)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |

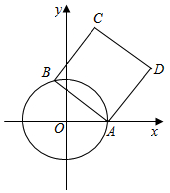 已知圆O为单位圆:x2+y2=1,点A(1,0),B为单位圆上的动点,如图,以AB为边作正方形ABCD,求动点D的轨迹方程及OD的取值范围.
已知圆O为单位圆:x2+y2=1,点A(1,0),B为单位圆上的动点,如图,以AB为边作正方形ABCD,求动点D的轨迹方程及OD的取值范围.