题目内容
在直角坐标系xOy中,点M(2,-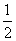 ),点F在抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分.
),点F在抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分.
(1)求m的值;
(2)过点M作直线l交抛物线C于A、B两点,设直线FA、FM、FB的斜率分别为k1、k2、k3,问k1、k2、k3能否成公差不为零的等差数列?若能,求直线l的方程;若不能,请说明理由.
(1)由题得抛物线C的焦点F的坐标为(0, ),线段MF的中点N(1,
),线段MF的中点N(1, -
- )在抛物线C上,
)在抛物线C上,
∴ -
- =m,8m2+2m-1=0,∴m=
=m,8m2+2m-1=0,∴m= (m=-
(m=-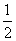 舍去).
舍去).
(2)由(1)知抛物线C:x2=4y,F(0,1).
设直线l的方程为y+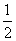 =k(x-2),A(x1,y1)、B(x2,y2),
=k(x-2),A(x1,y1)、B(x2,y2),
 假设k1、k2、k3能成公差不为零的等差数列,则k1+k3=2k2.
假设k1、k2、k3能成公差不为零的等差数列,则k1+k3=2k2.
 解得k=-
解得k=-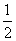 (符合题意)或k=-
(符合题意)或k=- (不合题意,舍去).
(不合题意,舍去).
∴直线l的方程为y+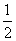 =-
=-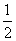 (x-2),
(x-2),
即x+2y-1=0.
∴k1、k2、k3能成公差不为零的等差数列,此时直线l的方程为x+2y-1=0.

练习册系列答案
相关题目
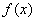 满足:①对任意实数
满足:①对任意实数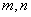 都有
都有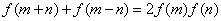 ;②对任意
;②对任意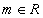 ,有
,有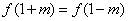 ;③
;③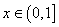 时,
时,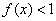 。
。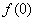 ,
,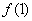 的值;
的值; 定义域中的任意一个
定义域中的任意一个 ,均有
,均有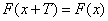 ,则称
,则称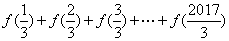 的值。
的值。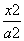 -
-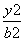 =1(a>0,b>0)的左、右焦点,若双曲线的右支上存在一点P,使
=1(a>0,b>0)的左、右焦点,若双曲线的右支上存在一点P,使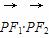 =0,且△F1PF2的三边长构成等差数列,则此双曲线的离心率为( )
=0,且△F1PF2的三边长构成等差数列,则此双曲线的离心率为( )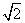 B.
B.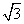
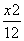 -
-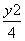 =1的渐近线的距离为( )
=1的渐近线的距离为( )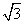
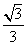 D.
D.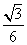
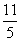 D.
D.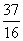
 取得最小值时的点P的坐标是______.
取得最小值时的点P的坐标是______.