题目内容
已知函数 在
在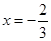 与
与 时都取得极值
时都取得极值
(1)求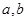 的值与函数
的值与函数 的单调区间
的单调区间
(2)若对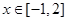 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。
【答案】
解:⑴ ,增区间
,增区间 减区间
减区间 ;
;
⑵ 或
或 。
。
【解析】本试题主要是考查了导数在研究函数极值和单调性中的运用,以及不等式的恒成立问题的综合运用。
(1)因为函数 在
在 与
与 时都取得极值,因此在这两点处的导数值为零的,得到参数a,b的值。并求解导数大于零或者小于零的区间。
时都取得极值,因此在这两点处的导数值为零的,得到参数a,b的值。并求解导数大于零或者小于零的区间。
(2)要满足对 ,不等式
,不等式 恒成立,只需要求解函数在给定区间的最大值小于
恒成立,只需要求解函数在给定区间的最大值小于 即可。
即可。
解:⑴
增区间 减区间
减区间 -------4分
-------4分
⑵∵对 ,不等式
,不等式 恒成立,
恒成立,
由(1)得


∴ 即
即 或
或 -------10分
-------10分

练习册系列答案
相关题目
 在
在 与
与 时都取得极值
时都取得极值 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。 在
在 与
与 时都取得极值
时都取得极值 的值 (2)若对
的值 (2)若对 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围
的取值范围  在
在 与
与 时都取得极值。
时都取得极值。 的值及函数
的值及函数 的单调区间;
的单调区间; 恒成立,求
恒成立,求 的取值范围。
的取值范围。 在
在 与
与 时都取得极值
时都取得极值 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。 在
在 与
与 时都取得极值.
时都取得极值. 的值及函数
的值及函数 的单调区间;
的单调区间; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.