题目内容
（满分14分）已知函数
在
与
时都取得极值
(1)求
的值与函数
的单调区间
(2)若对
，不等式
恒成立，求
的取值范围。
【答案】
（1）
，函数
的递增区间是
与
,递减区间是
；
（2）
。
【解析】解：（1）
由
，
得
，函数的单调区间如下表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
极大值 |
¯ |
极小值 |
|
所以函数的递增区间是与,递减区间是；
（2）
，当
时，
为极大值，而
，则为最大值，要使
恒成立，则只需要
，得。
练习册系列答案
相关题目
，如果满足；对任意
，存在常数
，都有
成立，则称
，
当
时，求函数
上的值域，并判断函数
上是以3为上界函数值，求实数
的取值范围；若
，求函数
在
上的上界T的取值范围。
.
的最小正周期；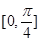
上的函数值的取值范围.
的单调性；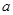
的取值范围；
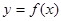对于区间D上的任意两个值x1、x2总有以下不等式
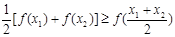成立，则称函数
，试判断函数
，如果满足；对任意
，存在常数
，都有
成立，则称
，
时，求函数
上的值域，并判断函数
上是以3为上界函数值，求实数
的取值范围；
，求函数
在
上的上界T的取值范围。
，如果满足；对任意
，存在常数
，都有
成立，则称
，
时，求函数
上的值域，并判断函数
上是以3为上界函数值，求实数
的取值范围；
，求函数
在
上的上界T的取值范围。