题目内容
如图所示,已知动直线![]() 经过点P(4,0)交抛物线
经过点P(4,0)交抛物线![]() 于A、B两点.
于A、B两点.
(1)以AP为直径作圆C,当圆心C到抛物线的准线的距离为多少时,圆的面积为7![]() ?
?
(2)是否存在垂直于![]() 轴的直线
轴的直线![]() 被以AP为直径的圆截得的弦长为定值?若存在,求出
被以AP为直径的圆截得的弦长为定值?若存在,求出![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
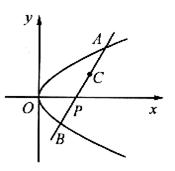
解:(1)设A1(![]() ),P(4,0).∴
),P(4,0).∴![]() ,
,
∴![]() ,从而|PA|=
,从而|PA|=![]() .
.
即![]() .
.
解得![]() 或
或![]() (舍去),A点的横坐标为6.
(舍去),A点的横坐标为6.
∴C点的横坐标为![]() .
.
此时圆心C到准线![]() 的距离是6.
的距离是6.
∴当圆心C到准线的距离是6时,圆C的面积为![]() .
.
(2)假设存在直线![]() :
:![]() 满足题意,设
满足题意,设![]() 交圆C于D,E两点,DE的中点为H,
交圆C于D,E两点,DE的中点为H,
设A(![]() ),|DC|=
),|DC|=![]() |AP|=
|AP|=![]() ,
,
而C(![]() ).
).
∴|CH|=![]()
|DH| 2=|CD|2-|CH|2
=![]()
=![]() .
.
∴当![]() =3时,|DH|2是与
=3时,|DH|2是与![]() 无关的常数.
无关的常数.
故存在直线![]() =3被以AP为直径的动圆截得的弦长为定值.
=3被以AP为直径的动圆截得的弦长为定值.

练习册系列答案
相关题目
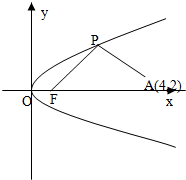 如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点.
如图所示,已知直线l的斜率为k且过点Q(-3,0),抛物线C:y2=16x,直线与抛物线l有两个不同的交点,F是抛物线的焦点,点A(4,2)为抛物线内一定点,点P为抛物线上一动点. 如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P. (理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足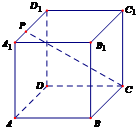 如图所示,已知点P是正方体ABCD-A1B1C1D1的棱A1D1上的一个动点,设异面直线AB与CP所成的角为α,则cosα的最小值是
如图所示,已知点P是正方体ABCD-A1B1C1D1的棱A1D1上的一个动点,设异面直线AB与CP所成的角为α,则cosα的最小值是