题目内容
已知：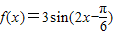
，x∈[0，
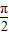]，求：（1）f（x）的最小正周期和单调增区间；
（2）求函数的最大值及最小值，并写出x取何值时函数有最大值和最小值．
【答案】分析：（1）根据复合三角函数的周期公式求得函数的最小正周期 T=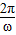
=
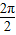，令 
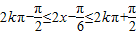，求得x的范围，再结合x∈[0，
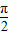]，可得函数的增区间．
（2）由x的范围以及函数的单调性，求得函数的最大值和最小值．
解答：解：（1）T=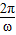
=
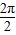=π，（2分），
令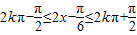
，求得
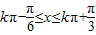，（5分）
再由x∈[0，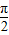
]，可得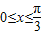
，即函数的增区间为[0，
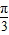]．（8分）
（2）由（1）可知：当x=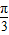
时，函数取得最大值3；当x=0时，函数取得最小值为-
．（14分）
点评：本题主要考查复合三角函数的单调性、周期性，正弦函数的定义域和值域，属于中档题．
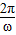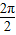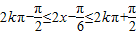=，令 ，求得x的范围，再结合x∈[0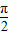，]，可得函数的增区间．（2）由x的范围以及函数的单调性，求得函数的最大值和最小值．
解答：解：（1）T=
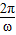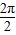==π，（2分），令
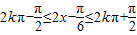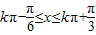，求得，（5分）再由x∈[0，
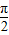]，可得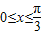，即函数的增区间为[0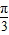，]．（8分）（2）由（1）可知：当x=
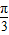时，函数取得最大值3；当x=0时，函数取得最小值为-．（14分）点评：本题主要考查复合三角函数的单调性、周期性，正弦函数的定义域和值域，属于中档题．
练习册系列答案
相关题目