题目内容
设 ,且
,且 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A.  B.
B. 
C.  D.
D. 
C
【解析】
试题分析:由 可得
可得 ,即可得
,即可得 .由于
.由于 .又
.又 .由正切函数的单调性可得
.由正切函数的单调性可得 ,即
,即 .故选C.
.故选C.
考点:1.三角函数的恒等变形.2.三角函数的单调性.
考点分析: 考点1:三角函数模型的应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
(本小题满分12分)
为了研究某种细菌在特定环境下,随时间变化繁殖情况,得如下实验数据:
天数t(天) | 3 | 4 | 5 | 6 | 7 |
繁殖个数y(千个) | 2.5 | 3 | 4 | 4.5 | 6 |
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,预测 时,细菌繁殖个数.
时,细菌繁殖个数.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
, .
.
 的不等式组
的不等式组 ,表示的平面区域是直角三角形区域,则正数
,表示的平面区域是直角三角形区域,则正数 的值为( )
的值为( ) 时,函数
时,函数 等于函数
等于函数 的导函数,若输入函数
的导函数,若输入函数 ,则输出的函数
,则输出的函数
 B.
B.
 D.
D.
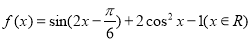 .
.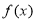 的单调递增区间;
的单调递增区间;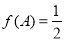 ,b,a,c成等差数列,且
,b,a,c成等差数列,且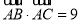 ,求a的值.
,求a的值. 上有两个动点P,Q,E(3,0)为定点,EP⊥EQ,则
上有两个动点P,Q,E(3,0)为定点,EP⊥EQ,则 最小值为( )
最小值为( ) C. 9 D.
C. 9 D. 
 ,
, ,则集合
,则集合 等于( )
等于( ) B.
B.  C.
C.  D.
D. 
 ,
, ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
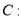
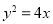 上一点
上一点 到
到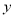 轴的距离为
轴的距离为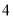 ,则点
,则点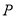 到抛物线
到抛物线 的焦点的距离是( )
的焦点的距离是( )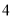 B.
B.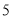 C.
C. D.
D.