题目内容
已知点F1、F2分别为双曲线
-
=1（a＞0，b＞0）的左、右焦点，P为双曲线左支上的任意一点，若
的最小值为9a，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、2 | B、5 | C、3 | D、2或5 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：首先利用双曲线的定义求出关系式，进一步利用
的最小值为9a，确定m=a或4a，此时c=2a或5a，即可求出双曲线的离心率．
| |PF2|2 |
| |PF1| |
解答：
解：设|PF1|=m，（m≥c-a）
则根据双曲线的定义：|PF2|=2a+m，
∴
=
=
+m+4a
∵
的最小值为9a，
∴m=a或4a，此时c=2a或5a，
∴双曲线的离心率为2或5，
双曲线的离心率为2时，不满足．
故选：B．
则根据双曲线的定义：|PF2|=2a+m，
∴
| |PF2|2 |
| |PF1| |
| (2a+m)2 |
| m |
| 4a2 |
| m |
∵
| |PF2|2 |
| |PF1| |
∴m=a或4a，此时c=2a或5a，
∴双曲线的离心率为2或5，
双曲线的离心率为2时，不满足．
故选：B．
点评：本题考查双曲线的定义、双曲线的离心率，考查学生的计算能力，属于中等题型．
练习册系列答案
名校课堂系列答案
相关题目
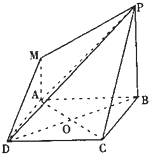如图，四边形ABCD是正方形，MA⊥平面ABCD，MA∥PB，PB=AB=2MA=2．
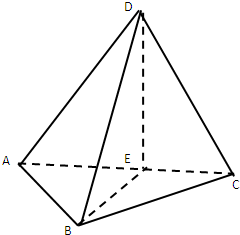如图，三棱锥D-ABC中，AB=BC=2，BD=3，∠ABC=∠DBA=∠DBC=60°，E为AC的中点．