题目内容
如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.

(Ⅰ)求证:A,M,B三点的横坐标成等差数列;
(Ⅱ)已知当M点的坐标为(2,-2p)时,![]() 求此时抛物线的方程;
求此时抛物线的方程;
(Ⅲ)是否存在点M,使得点C关于直线AB的对称点D在抛物线x2=2py(p>0)上,其中点C满足![]() (O为坐标原点).若存在,求出所有适合题意的点的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点的坐标;若不存在,请说明理由.
解析:
|
标准答案: (Ⅰ)证明:由题意设 由 所以 因此直线 直线 所以 由①、②得 因此 所以 (Ⅱ)解:由(Ⅰ)知,当 将其代入①、②并整理得: 所以 因此 又 所以 由弦长公式得 又 因此所求抛物线方程为 (Ⅲ)解:设 则 设直线 由点 代入得 若 因此 即 (1)当 (2)当 又 所以 即 对于 又 所以直线 所以 综上所述,仅存在一点 试题分析:(Ⅰ)设 (Ⅱ)利用弦长公式求的关于 (Ⅲ) 高考考点:直线和圆锥曲线的位置关系 |
提示:
|
解析几何问题有很强的程序性,题目的类型也相对集中,如弦长、中点弦、动点轨迹、定点与定值、取值与最值、圆锥曲线与向量等问题,计算繁琐但有序.只要掌握圆锥曲线的定义和性质明确解决直线与圆锥曲线位置关系的思想方法,沟通知识间的横纵联系,借助方程与不等式以及向量工具,适当选择数形结合思想、转化思想,很多相关问题就能迎难而解. |

 .
. ,
, .
. ,
,
 ,因为
,因为 ,此时直线
,此时直线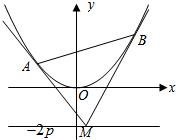 如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B. 如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.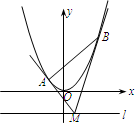 如图,设抛物线方程为x2=2py(p>0),M为直线l:y=-2p上任意一点,过M引抛物线的切线,切点分别为A、B.
如图,设抛物线方程为x2=2py(p>0),M为直线l:y=-2p上任意一点,过M引抛物线的切线,切点分别为A、B. ,
, 为直线
为直线 上任意一点,过
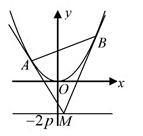
上任意一点,过 .
.
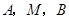 三点的横坐标成等差数列;
三点的横坐标成等差数列;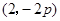 时,
时,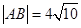 .求此时抛物线的方程。
.求此时抛物线的方程。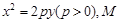 直线
直线 上任意一点,过M引抛物线的切线,切点分别为A,B。
上任意一点,过M引抛物线的切线,切点分别为A,B。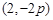 时,
时,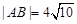 ,求此时抛物线的方程;
,求此时抛物线的方程; 上,其中,点C满足
上,其中,点C满足 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.