题目内容
如图,设抛物线方程为 ,
,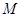 为直线
为直线 上任意一点,过
上任意一点,过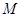 引抛物线的切线,切点分别为
引抛物线的切线,切点分别为 .
.
(1)求证: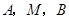 三点的横坐标成等差数列;
三点的横坐标成等差数列;
(2)已知当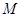 点的坐标为
点的坐标为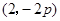 时,
时,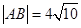 .求此时抛物线的方程。
.求此时抛物线的方程。
【答案】
(1)根据已知条件设出点A,B的坐标,,然后借助于抛物线的导数来得到斜率值 ,
,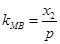 .,进而解方程,得到证明。
.,进而解方程,得到证明。
(2)抛物线方程为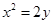 或
或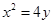 .
.
【解析】
试题分析:(1)证明:由题意设 .
.
由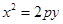 得
得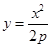 ,得
,得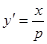 ,所以
,所以 ,
,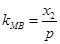 .
.
因此直线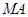 的方程为
的方程为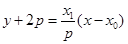 ,
,
直线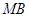 的方程为
的方程为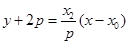 .
.
所以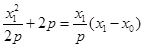 ,①
,① 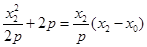 .②
.②
由①减②得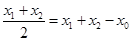 ,因此
,因此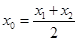 ,即
,即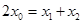 .
.
所以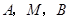 三点的横坐标成等差数列.
6分
三点的横坐标成等差数列.
6分
(2)由(1)知,当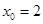 时,将其代入①、②并整理得:
时,将其代入①、②并整理得:
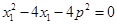 ,
,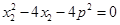 ,
,
所以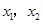 是方程
是方程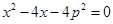 的两根,
的两根,
因此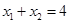 ,
,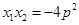 ,
,
又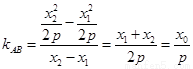 ,所以
,所以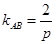 .
.
由弦长公式得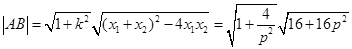 .
.
又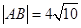 ,所以
,所以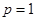 或
或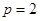 ,
,
因此所求抛物线方程为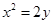 或
或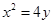 . 12分
. 12分
考点:直线与抛物线的位置关系
点评:解决的关键是利用直线与抛物线的相切得到切线的斜率,同时联立方程组求解弦长,属于中档题。

练习册系列答案
相关题目
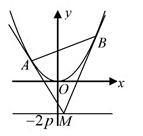
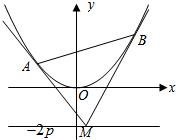 如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B. 如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
如图,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.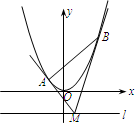 如图,设抛物线方程为x2=2py(p>0),M为直线l:y=-2p上任意一点,过M引抛物线的切线,切点分别为A、B.
如图,设抛物线方程为x2=2py(p>0),M为直线l:y=-2p上任意一点,过M引抛物线的切线,切点分别为A、B.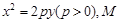 直线
直线 上任意一点,过M引抛物线的切线,切点分别为A,B。
上任意一点,过M引抛物线的切线,切点分别为A,B。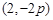 时,
时,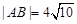 ,求此时抛物线的方程;
,求此时抛物线的方程; 上,其中,点C满足
上,其中,点C满足 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.