题目内容
（1）在直角坐标系中，已知三点A（5，4），B（k，10），C（12，-2），当k为何值时，向量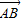
与
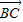共线？（2）在直角坐标系中，已知O为坐标原点，
，
，
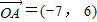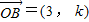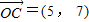，当k为何值时，向量
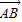与
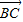垂直？
【答案】分析：（1）由点的坐标求出对应向量的坐标，然后利用向量共线的坐标表示列式求解；
（2）由点的坐标求出对应向量的坐标，然后利用向量垂直的坐标表示列式求解
解答：解：（1）∵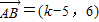
，
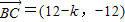
又向量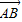
与
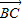共线
∴（k-5）×（-12）-（12-k）×6=0
解得 k=-2；
（2）∵
，
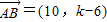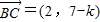
又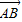
⊥
，∴
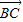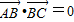
∴20+（k-6）（7-k）=0，
解得 k=2或 k=11．
点评：本题考查了平面向量平行的坐标表示，考查了平面向量垂直的条件，是基础的运算题．
（2）由点的坐标求出对应向量的坐标，然后利用向量垂直的坐标表示列式求解
解答：解：（1）∵
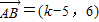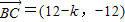
，又向量
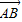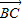与共线∴（k-5）×（-12）-（12-k）×6=0
解得 k=-2；
（2）∵
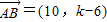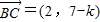
，又
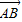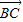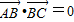
⊥，∴∴20+（k-6）（7-k）=0，
解得 k=2或 k=11．
点评：本题考查了平面向量平行的坐标表示，考查了平面向量垂直的条件，是基础的运算题．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
（2009•奉贤区一模）已知函数
设