Question

设f(x)=

x+2(x≤-1) x2(-1＜x＜2) 2x(x≥2)

，
（1）在直角坐标系中画出f（x）的图象；
（2）求f[f （-

3

2

）]的值；
（3）若f （x）=3，求x值．

Answer 1

分析：（1）建立直角坐标系，分别根据每段的解析式画出图象；
（2）根据每段的解析式，分别代入，即可求得f[f （-

3

2

）]的值；
（3）对x进行分类讨论，依次列出方程求解，即可求得x的值．

解答：解：（1）作出图象如图所示；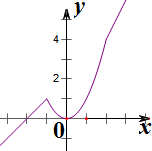
（2）∵-

3

2

＜-1，
∴f（-

3

2

）=-

3

2

+2=

1

2

，
∴f[f （-

3

2

）]=f（

1

2

）=（

1

2

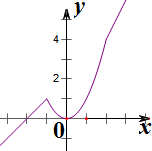
）²=

1

4

，
故f[f （-

3

2

）]的值为

1

4

；
（3）∵f(x)=

x+2(x≤-1) x2(-1＜x＜2) 2x(x≥2)

，
①当x≤-1时，f（x）=x+2=3，解得x=1，不符合题意；
②当-1＜x＜2时，f（x）=x²=3，解得x=±

3

，
∵-1＜x＜2，则x=

3

；
③当x≥2时，f（x）=2x=3，解得x=

3

2

，不符合题意；
综合①②③，可得x=

3

．

点评：本题考查了分段函数的解析式及其图象的作法，考查了分段函数的取值问题，分段函数的零点问题．对于分段函数一般选用数形结合和分类讨论的数学思想进行解题．属于基础题．