题目内容
设函数 .
.
(1)若 ,且
,且 ,求
,求 的值;
的值;
(2)若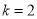 ,记函数
,记函数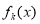 在
在 上的最大值为
上的最大值为 ,最小值为
,最小值为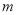 ,求
,求 时的
时的 的取值范围;
的取值范围;
(3)判断是否存在大于1的实数 ,使得对任意
,使得对任意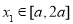 ,都有
,都有 满足等式:
满足等式: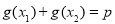 ,且满足该等式的常数
,且满足该等式的常数 的取值唯一?若存在,求出所有符合条件的
的取值唯一?若存在,求出所有符合条件的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)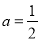 ;(2)
;(2)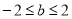 ;(3)
;(3)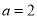 .
.
【解析】
试题分析:(1)代入求解即可;(2)讨论二次函数的对称轴与区间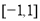 的关系取得最大值与最小值,再解关于
的关系取得最大值与最小值,再解关于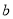 的不等式即可;(3)将问题转化为集合间的包含关系,利用唯一性求解.
的不等式即可;(3)将问题转化为集合间的包含关系,利用唯一性求解.
解题思路:当二次函数的系数含有字母时,求其值域要分类讨论,讨论它的开口方向、对称轴与给定区间的关系.
试题解析:(1)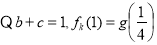 ,
,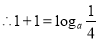 ,解得
,解得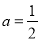 ;
;
若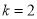 ,则
,则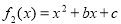 的开口向上,对称轴方程为
的开口向上,对称轴方程为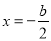 ;
;
当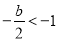 ,即
,即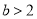 时,
时,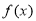 在
在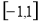 单调递增,则
单调递增,则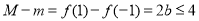 ,即
,即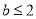 (舍);
(舍);
当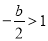 ,即
,即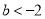 时,
时,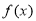 在
在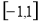 单调递减,则
单调递减,则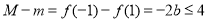 ,即
,即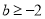 (舍);
(舍);
当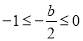 ,即
,即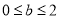 时,
时,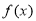 在
在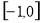 单调递减,在
单调递减,在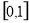 单调递增,
单调递增,
则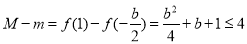 ,即
,即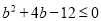 ,解得
,解得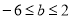 ,即
,即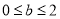 ;
;
当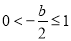 ,即
,即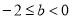 时,
时,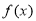 在
在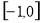 单调递减,在
单调递减,在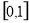 单调递增,
单调递增,
则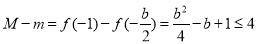 ,即
,即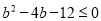 ,解得
,解得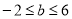 ,即
,即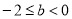 ;
;
综上所述,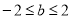 ;
;
由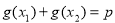 ,得
,得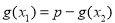 ,由题意,得
,由题意,得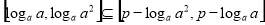 ,
,
即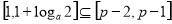 ,即
,即 ,即
,即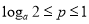 ,因为满足该等式的常数
,因为满足该等式的常数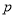 的取值唯一,所以
的取值唯一,所以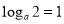 ,解得
,解得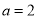 .
.
考点:1.对数的运算;2.二次函数的值域;3.分类讨论思想.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 满足条件
满足条件 ,则
,则 的最小值为
的最小值为 B.0 C.
B.0 C. D.
D.
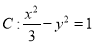 的左,右焦点分别为
的左,右焦点分别为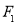 ,
,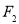 ,过点
,过点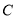 的右支相交于
的右支相交于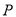 ,
,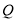 两点,且点
两点,且点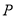 的横坐标为
的横坐标为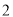 ,则△
,则△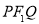 的周长为( )
的周长为( )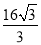 B.
B.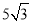 C.
C.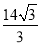 D.
D.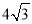
 的定义域为集合
的定义域为集合 ,函数
,函数 的值域为集合
的值域为集合 ,
,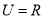 .
.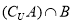 ;
;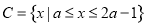 且
且 ,求实数
,求实数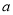 的取值范围,
的取值范围,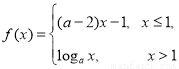 若
若 在
在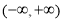 上单调递增,则实数
上单调递增,则实数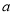 的取值范围为
的取值范围为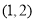 B.
B.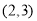 C.
C.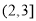 D.
D.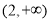
 的单调递增区间是
的单调递增区间是  中,若
中,若 ,则
,则