题目内容
 如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,BC⊥CF,AD=
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,BC⊥CF,AD=| 3 |
(Ⅰ)求证:EF⊥平面DCE;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为60°.
分析:(I)由已知中在△BCE中,BC⊥CF,BC=AD=
,BE=3,由勾股定理,我们易得EF⊥CE,由矩形ABCD和梯形BEFC所在平面互相垂直,可得DC⊥平面EFCB,则DC⊥EF,进而由线面垂直的判定定理得到答案.
(II)方法一(几何法)过点B作BH⊥EF交FE的延长线于H,连接AH,由三垂线定理及二面角的平面角的定义,易得∠AHB为二面角A-EF-C的平面角,解Rt△CEF,即可求出二面角A-EF-C的大小为60°时,AB的长.
方法二(向量法)以点C为坐标原点,以CB,CF和CD分别作为x轴,y轴和z轴,建立空间直角坐标系C-xyz,设AB=a,分别求出平面AEF的法向量和平面EFCB的法向量,代入向量夹角公式,由二面角A-EF-C的大小为60°,构造关于a的方程,解方程求出a值.
| 3 |
(II)方法一(几何法)过点B作BH⊥EF交FE的延长线于H,连接AH,由三垂线定理及二面角的平面角的定义,易得∠AHB为二面角A-EF-C的平面角,解Rt△CEF,即可求出二面角A-EF-C的大小为60°时,AB的长.
方法二(向量法)以点C为坐标原点,以CB,CF和CD分别作为x轴,y轴和z轴,建立空间直角坐标系C-xyz,设AB=a,分别求出平面AEF的法向量和平面EFCB的法向量,代入向量夹角公式,由二面角A-EF-C的大小为60°,构造关于a的方程,解方程求出a值.
解答: 证明:(Ⅰ)在△BCE中,BC⊥CF,BC=AD=
证明:(Ⅰ)在△BCE中,BC⊥CF,BC=AD=
,BE=3,∴EC=2
,
∵在△FCE中,CF2=EF2+CE2,∴EF⊥CE(3分)由已知条件知,DC⊥平面EFCB,
∴DC⊥EF,又DC与EC相交于C,(5分)∴EF⊥平面DCE(6分)
解:(Ⅱ)
方法一:过点B作BH⊥EF交FE的延长线于H,连接AH.
由平面ABCD⊥平面BEFC,平面ABCD∩平面BEFC=BC,
AB⊥BC,得AB⊥平面BEFC,从而AH⊥EF.
所以∠AHB为二面角A-EF-C的平面角.(8分)
在Rt△CEF中,因为EF=2,CF=4.EC=2

∴∠CEF=90°,由CE∥BH,得∠BHE=90°,又在Rt△BHE中,BE=3,
∴BH=BE•sin∠BEH=
(10分)
由二面角A-EF-C的平面角∠AHB=60°,在Rt△AHB中,解得AB=BH•tan∠AHB=
,
所以当AB=
时,二面角A-EF-C的大小为60°(13分)
方法二:如图,以点C为坐标原点,以CB,CF和CD分别作为x轴,y轴和z轴,建立空间直角坐标系C-xyz.(7分)
设AB=a(a>0),则C(0,0,0),A(
,0,a),B(
,0,0),E(
,3,0),F(0,4,0).
从而
=(-
,1,0),
=(0,3,-a),(9分)
设平面AEF的法向量为
=(x,y,z),由
•
=0,
•
=0得,
,取x=1,
则y=
,z=
,即
=(1,
,
),(11分)
不妨设平面EFCB的法向量为
=(0,0,a),
由条件,得|cos<
,
>|=|
|=
=
解得a=
.所以当AB=
时,二面角A-EF-C的大小为60°.(13分)
 证明:(Ⅰ)在△BCE中,BC⊥CF,BC=AD=
证明:(Ⅰ)在△BCE中,BC⊥CF,BC=AD=| 3 |
| 3 |
∵在△FCE中,CF2=EF2+CE2,∴EF⊥CE(3分)由已知条件知,DC⊥平面EFCB,
∴DC⊥EF,又DC与EC相交于C,(5分)∴EF⊥平面DCE(6分)
解:(Ⅱ)
方法一:过点B作BH⊥EF交FE的延长线于H,连接AH.
由平面ABCD⊥平面BEFC,平面ABCD∩平面BEFC=BC,
AB⊥BC,得AB⊥平面BEFC,从而AH⊥EF.
所以∠AHB为二面角A-EF-C的平面角.(8分)
在Rt△CEF中,因为EF=2,CF=4.EC=2
| 3 |

∴∠CEF=90°,由CE∥BH,得∠BHE=90°,又在Rt△BHE中,BE=3,
∴BH=BE•sin∠BEH=
3
| ||
| 2 |
由二面角A-EF-C的平面角∠AHB=60°,在Rt△AHB中,解得AB=BH•tan∠AHB=
| 9 |
| 2 |
所以当AB=
| 9 |
| 2 |
方法二:如图,以点C为坐标原点,以CB,CF和CD分别作为x轴,y轴和z轴,建立空间直角坐标系C-xyz.(7分)
设AB=a(a>0),则C(0,0,0),A(
| 3 |
| 3 |
| 3 |
从而
| EF |
| 3 |
| AE |
设平面AEF的法向量为
| n |
| EF |
| n |
| AE |
| n |
|
则y=
| 3 |
3
| ||
| a |
| n |
| 3 |
3
| ||
| a |
不妨设平面EFCB的法向量为
| BA |
由条件,得|cos<
| n |
| BA |
| ||||
|
|
3
| ||
a
|
| 1 |
| 2 |
解得a=
| 9 |
| 2 |
| 9 |
| 2 |
点评:本题考查的知识点是用空间向量求平面间的夹角,其中(I)的关键是熟练掌握线线垂直、线面垂直与面面垂直的之间的相互转化,(II)的关键是建立空间坐标系,将二面角问题,转化为向量的夹角问题.

练习册系列答案
相关题目
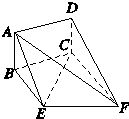 如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=
如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD= 如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF=
如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF= 如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°,
如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°, 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD= 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=