Question

【题目】数列{an}首项a1＝1，前n项和Sn与an之间满足an＝

（1）求证：数列{}是等差数列

（2）求数列{an}的通项公式

（3）设存在正数k，使（1+S1）（1+S2）…（1+Sn）≥k对于一切n∈N*都成立，求k的最大值．

Answer 1

【答案】(1)证明见详解；(2)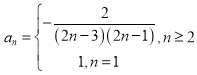；(3).

【解析】

（1）利用与之间的关系，将an＝转化为和之间的关系式，再整理即可求得；

（2）根据（1）中所证可得，根据与的联系即可求得；

（3）构造数列，判断其单调性，再求最小值即可求得参数的取值范围.

（1）因为，故an＝即为

整理可得

故可得，

故数列{}是以首项为1公差为2的等差数列，即证.

（2）由（1）可知，故可得

代入an＝，即可得

又当时，不满足上式，

故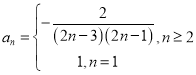

（3）由（1）可知，设

故可得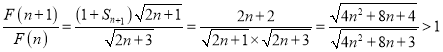

故是单调递增数列，则，

要满足（1+S1）（1+S2）…（1+Sn）≥k对于一切n∈N*都成立

只需，即可得.

故的最大值为：.