题目内容
【题目】已知函数![]() 有两个零点
有两个零点![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)记![]() 的极值点为
的极值点为![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)求导得![]() ,分类讨论求出函数的单调性,从而可求出答案;
,分类讨论求出函数的单调性,从而可求出答案;
(2)由题意得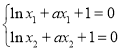 ,则
,则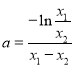 ,令函数
,令函数![]() ,则
,则![]() ,利用导数可求得
,利用导数可求得![]() ,从而可得
,从而可得![]() ,可得
,可得![]() ,要证
,要证![]() ,只需
,只需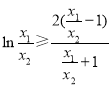 ,令
,令![]() ,即证
,即证![]() ,令
,令![]() ,求导后得函数的单调性与最值,由此可证结论.
,求导后得函数的单调性与最值,由此可证结论.
解:(1)因为![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增,至多只有一个零点,不符合题意,舍去;
单调递增,至多只有一个零点,不符合题意,舍去;
当![]() 时,若
时,若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
所以![]() ,
,
因为![]() 有两个零点,所以必须
有两个零点,所以必须![]() ,则
,则![]() ,
,
所以![]() ,解得
,解得![]() ,
,
又因为![]() 时,
时,![]() ;
; ![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 在
在![]() 和
和![]() 各有一个零点,符合题意,
各有一个零点,符合题意,
综上,![]() ;
;
(2)由(1)知![]() ,且
,且![]() ,
,
因为![]() 的两个零点为
的两个零点为![]() ,所以
,所以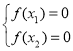 ,所以
,所以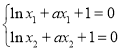 ,
,
解得![]() ,令
,令![]() 所以
所以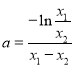 ,
,
令函数![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
因为![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,
,
要证![]() ,只需
,只需![]() ,
,
即证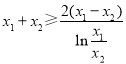 ,即证
,即证![]() ,即证
,即证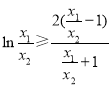 ,
,
令![]() ,再令
,再令![]() ,即证
,即证![]() ,
,
令![]() ,则
,则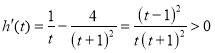 ,
,
所以![]() 在
在![]() 单调递增,所以
单调递增,所以![]() ,
,
所以![]() ,原题得证.
,原题得证.

【题目】某地区人民法院每年要审理大量案件,去年审理的四类案件情况如表所示:
编号 | 项目 | 收案(件) | 结案(件) | |
判决(件) | ||||
1 | 刑事案件 | 2400 | 2400 | 2400 |
2 | 婚姻家庭、继承纠纷案件 | 3000 | 2900 | 1200 |
3 | 权属、侵权纠纷案件 | 4100 | 4000 | 2000 |
4 | 合同纠纷案件 | 14000 | 13000 | n |
其中结案包括:法庭调解案件、撤诉案件、判决案件等.根据以上数据,回答下列问题.
(Ⅰ)在编号为1、2、3的收案案件中随机取1件,求该件是结案案件的概率;
(Ⅱ)在编号为2的结案案件中随机取1件,求该件是判决案件的概率;
(Ⅲ)在编号为1、2、3的三类案件中,判决案件数的平均数为![]() ,方差为S12,如果表中n
,方差为S12,如果表中n![]() ,表中全部(4类)案件的判决案件数的方差为S22,试判断S12与S22的大小关系,并写出你的结论(结论不要求证明).
,表中全部(4类)案件的判决案件数的方差为S22,试判断S12与S22的大小关系,并写出你的结论(结论不要求证明).