题目内容
已知点 M(-2,0),N(2,0),动点 P满足条件|PM |-|PN|=(1)求 W的方程;
(2)若 A,B是W上的不同两点,O是坐标原点,求的![]() 最小值.
最小值.
思路分析:本题考查圆锥曲线方程的解法及最值问题的解决.记住一些有用的解题的小结论、小技巧,也许对提高解题的速度是有较大的帮助的.
解:(1)由|PM|-|PN|=![]() 知,动点P的轨迹是以为M、N焦点的双曲线的右支,实半轴长a=
知,动点P的轨迹是以为M、N焦点的双曲线的右支,实半轴长a=![]() .
.
又半焦距c=2,故虚半轴b=![]() .
.
所以W的方程为![]() =1,x≥
=1,x≥![]() .
.
(2)设 A,B的坐标分别为(x1,y1),(x2,y2),
当AB⊥x轴时,x1=x2,从而y1=y2,从而![]() =x1x2+y1y2=x12-y12=2.
=x1x2+y1y2=x12-y12=2.
当AB与x轴不垂直时,设直线AB的方程为y=kx+m,与W的方程联立,消去y得(1-k2)x2-2kmx-m2-2=0.
故x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
所以![]() =x1x2+y1y2=x1x2+(kx1+m)(kx2+m)
=x1x2+y1y2=x1x2+(kx1+m)(kx2+m)
=(1+k2)x1x2+km(x1+x2)+m2=![]() +m2=
+m2=![]() .
.
又因为x1x2>0,所以k2-1>0,从而![]() >2
>2
综上,当AB⊥x轴时,![]() 取得最小值2.
取得最小值2.

练习册系列答案
相关题目
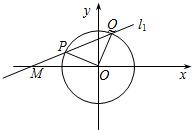 已知点M(-2,0),⊙O:x2+y2=1(如图);若过点M的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的
已知点M(-2,0),⊙O:x2+y2=1(如图);若过点M的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的