题目内容
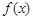 是定义在D上的函数,若存在区间
是定义在D上的函数,若存在区间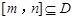 ,使函数
,使函数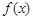 在
在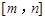 上的值域恰为
上的值域恰为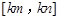 ,则称函数
,则称函数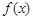 是k型函数.给出下列说法:
是k型函数.给出下列说法:①
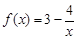 不可能是k型函数;
不可能是k型函数;②若函数
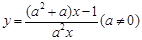 是1型函数,则
是1型函数,则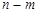 的最大值为
的最大值为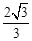 ;
;③若函数
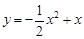 是3型函数,则
是3型函数,则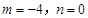 ;
;④设函数
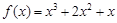 (x≤0)是k型函数,则k的最小值为
(x≤0)是k型函数,则k的最小值为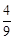 .
.其中正确的说法为 .(填入所有正确说法的序号)
②③
试题分析:由题意知
 .当存在直线
.当存在直线 与曲线
与曲线 至少有两个交点时,函数
至少有两个交点时,函数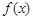 就是k型函数.对①,作出
就是k型函数.对①,作出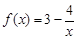 的图象即可知,
的图象即可知,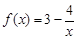 是k型函数;
是k型函数;对②,若函数
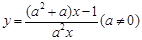 是1型函数,则
是1型函数,则 有两个不同的解,即
有两个不同的解,即 有两个不同的解
有两个不同的解 .由
.由 得
得 ,所以
,所以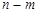
 (
( 时取等号),所以
时取等号),所以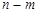 的最大值为
的最大值为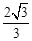 ;
;对③,若函数
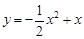 是3型函数,则
是3型函数,则 ,即
,即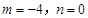 ;
;对④,作出
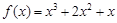 的图象,极值点
的图象,极值点 ,
, ,
, ,
, .由图可知,
.由图可知, 时,是
时,是 型函数.
型函数.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目

 与
与


 为偶函数,当
为偶函数,当 时,
时, ,满足
,满足 的实数
的实数 的个数为( )
的个数为( )
 满足
满足 ,且
,且 .
. 时,函数
时,函数 的图像恒在函数
的图像恒在函数 的图像的上方,求实数
的图像的上方,求实数 的取值范围.
的取值范围. 小时内供水总量为
小时内供水总量为 吨(
吨( ),从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
),从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?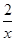 的零点,则[x0]=________.
的零点,则[x0]=________.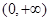 上单调递增的是( )
上单调递增的是( )



 、
、 ,运算“
,运算“ ”、“
”、“ ”定义为:
”定义为: =
= ,
, =
= ,则下列各式其中不恒成立的是( )
,则下列各式其中不恒成立的是( ) ⑵
⑵
 ⑷
⑷
 ,在区间
,在区间 内存在
内存在 使
使 ,则
,则 的取值范围是( )
的取值范围是( )


