题目内容
11.已知函数f(x)=|x-a|+|x-1|,a∈R.(Ⅰ)当a=3时,求不等式f(x)≤4的解集;
(Ⅱ)不等式f(x)<2的解集为空集,求实数a的取值范围.
分析 (Ⅰ)求出当a=3时,f(x)的分段函数式,原不等式即化为一次不等式组,分别解得它们,再求并集即可;
(Ⅱ)利用绝对值三角不等式可得f(x)=|x-a|+|x-1|≥|(x-a)+(1-x)|=|1-a|,依题意可得|1-a|≥2,解之即可.
解答 解:(Ⅰ)当a=3时,f(x)=|x-3|+|x-1|,
即有f(x)=$\left\{\begin{array}{l}{4-2x,x<1}\\{2,1≤x<3}\\{2x-4,x≥3}\end{array}\right.$,
不等式f(x)≤4即为$\left\{\begin{array}{l}{x<1}\\{4-2x≤4}\end{array}\right.$或$\left\{\begin{array}{l}{x≥3}\\{2x-4≤4}\end{array}\right.$或$\left\{\begin{array}{l}{1≤x<3}\\{2≤4}\end{array}\right.$,
即有0≤x<1或3≤x≤4或1≤x<3,
则为0≤x≤4,
则解集为[0,4];
(Ⅱ)依题意知,f(x)=|x-a|+|x-1|≥2恒成立,
∴2≤f(x)min;
由绝对值三角不等式得:f(x)=|x-a|+|x-1|≥|(x-a)+(1-x)|=|1-a|,
即f(x)min=|1-a|,
∴|1-a|≥2,即a-1≥2或a-1≤-2,
解得a≥3或a≤-1.
∴实数a的取值范围是[3,+∞)∪(-∞,-1].
点评 本题考查绝对值不等式的解法,求得|1-a|≥2是关键,突出考查等价转化思想和分类讨论思想与运算求解能力,属于中档题.

练习册系列答案
相关题目
3.执行如图所示的程序框图,则输出S的值是( )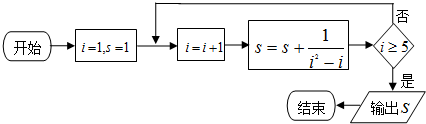

| A. | $\frac{4}{5}$ | B. | $\frac{9}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{11}{6}$ |
16.若复数$\frac{a+3i}{1+2i}$(α∈R,i为虚数单位)是纯虚数,则实数α的值为( )
| A. | -6 | B. | -4 | C. | 4 | D. | 6 |
20.抛物线y=-4x2的准线方程为( )
| A. | x=1 | B. | y=1 | C. | x=$\frac{1}{16}$ | D. | y=$\frac{1}{16}$ |
