题目内容

已知函数fn(x)(n∈N*)具有下列性质：

①fn(0)=，

②n[fn()-fn(]=[fn()-1]fn()(k=0,1，…，n-1)

(Ⅰ)当n一定时，记作ak=,求ak的表达式(k=0,1,…,n);

(Ⅱ)对n∈N*，证明＜fn(1)≤.

答案：(Ⅰ)

∴

即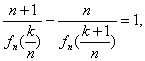∴(n+1)ak-nak+1=1,

∴n(ak+1-1)=(n+1)(ak-1),即由n为定值,则数列{ak-1}是以a0-1为首项.1+为公比的等比数列,∴ak-l=(a0-1)(1+)k,

由于a0=

(Ⅱ)∴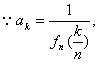

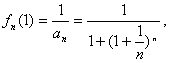
欲证

只需证明2≤(1+)n<3,


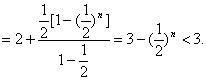
练习册系列答案
相关题目
已知函数fn(x)=(1+
1
n
)x（n∈N*）．
（Ⅰ）比较fn′（0）与
1
n
的大小；
（Ⅱ）求证：
f1′(1)
2
+
f2′(2)
3
+
f3′(3)
4
+…+
fn′(n)
n+1
＜3．
已知函数fn(x)=x2+x+
12
的定义域是[n，n+1]（n是自然数），那么f1（x）的值域中共有
4
4
个整数；fn（x）的值域中共有
2n+2
2n+2
个整数．
已知函数fn(x)=
ln(x+n)-n
x+n
+
1
n(n+1)
（其中n为常数，n∈N*），将函数fn（x）的最大值记为an，由an构成的数列{an}的前n项和记为Sn．
（Ⅰ）求Sn；
（Ⅱ）若对任意的n∈N*，总存在x∈R+使
x
ex-1
+a=an，求a的取值范围；
（Ⅲ）比较
1
en+1+e•n
+fn(en)与an的大小，并加以证明．
（2011•合肥三模）已知函数fn(x)=
1
3
x3-
1
2
(n+1)x2+x(n∈N*)，数列{an}满足an+1=f'n（an），a1=3．
（1）求a2，a3，a4；
（2）根据猜想数列{an}的通项公式，并证明；
（3）求证：
1
(2a1-5)2
+
1
(2a2-5)2
+…+
1
(2an-5)2
＜
3
2
．

已知函数fn(x)＝(1＋x)n－1，（n∈N*，且n＞1）．

(Ⅰ) 设函数，求的最大值和最小值

(Ⅱ) 若求证：fn(x)≥nx.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网