题目内容
已知 a,b满足a+2b=1,则直线ax+3y+b=0必过定点( )
A. | B. |
C. | D. |
B
解析试题分析:因为a,b满足a+2b=1,则直线ax+3y+b=0化为(1-2b)x+3y+b=0,即x+3y+b(-2x+1)=0恒成立, 得:
得: ,所以直线经过定点
,所以直线经过定点 。故选B.
。故选B.
考点:直线系方程。
点评:(1)平行直线系:与Ax+By+C=0平行的直线为:Ax+By+C1=0(C1≠C)。
(2)垂直直线系:与Ax+By+C=0垂直的直线为:Bx-Ay+C1=0。
(3)定点直线系:若 :
: =0和
=0和 :
: =0相交,则过
=0相交,则过 与
与 交点的直线系为
交点的直线系为 +λ
+λ =0。
=0。

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
设 满足
满足 则
则 ( )
( )
| A.有最小值2,最大值3 | B.有最小值2,无最大值 |
| C.有最大值3,无最小值 | D.既无最小值,也无最大值 |
已知点 在圆
在圆 上运动,则
上运动,则 的最大值与最小值为( )
的最大值与最小值为( )
A. , , | B. | C.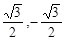 | D. |
设变量 满足约束条件
满足约束条件 则目标函数
则目标函数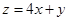 的最大值为( )
的最大值为( )
| A.4 | B.11 | C.12 | D.14 |
若实数 满足
满足 ,则
,则 的最大值是( )
的最大值是( )
A.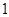 | B. | C. | D. |
已知实数 满足
满足 则
则 的最小值等于
的最小值等于
| A.0 | B.1 | C.2 | D.3 |
设函数 ,则满足
,则满足 的x的取值范围是
的x的取值范围是
A. ,2] ,2] | B.[0,2] | C.[1,+ ) ) | D.[0,+ ) ) |
在直角坐标系中,满足不等式 的点
的点 的集合(用阴影表示)是( )
的集合(用阴影表示)是( ) 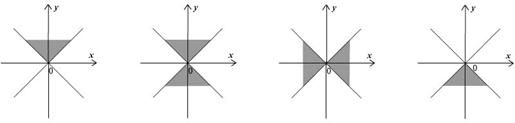
| A. | B. | C. | D. |
已知 满足
满足 ,且
,且 能取到最小值,则实数
能取到最小值,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.-1<a<2 |