题目内容
设函数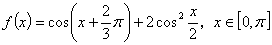 。
。
(1)求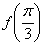 的值;
的值;
(2)求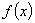 的最小值及
的最小值及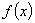 取最小值时
取最小值时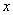 的集合;
的集合;
(3)求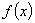 的单调递增区间。
的单调递增区间。
解:(1) 。
。
(2)


 。
。
因为 ,所以
,所以 ,所以
,所以 。
。
所以函数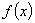 的最小值为0。
的最小值为0。
此时 ,即
,即 。所以
。所以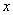 的取值集合为
的取值集合为 。
。
(3)由(2)可知: 。
。
设 ,则原函数为
,则原函数为 。
。
因为 为减函数,所以
为减函数,所以 的减区间就是复合函数
的减区间就是复合函数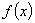 的增区间。
的增区间。
由 ,得
,得 。
。
所以,函数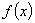 的单调递增区间是
的单调递增区间是 。
。

练习册系列答案
相关题目
 的直线
的直线 与曲线
与曲线 有公共点,则直线
有公共点,则直线 与两坐标轴无公共点,那么实数
与两坐标轴无公共点,那么实数 的取值范围是
的取值范围是 
 B.
B. C.
C.  D.
D.
 ,使得方程
,使得方程 在
在 上有两个不相等的实数根
上有两个不相等的实数根 ,则
,则 的值为
的值为 B. 0 C.1 D.
B. 0 C.1 D. 
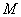 是
是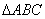 内的一点,且
内的一点,且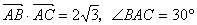 。定义:
。定义:
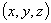 ,其中
,其中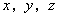 分别为
分别为 的面积,若
的面积,若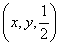 ,则
,则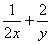 的最小值为______________________,此时
的最小值为______________________,此时 ( )
( ) B.
B. C.1 D.
C.1 D.
 的三视图如图1所示,则四棱锥
的三视图如图1所示,则四棱锥 B.
B. C.
C. D.
D.
