题目内容
已知数列 中,
中, ,
, .
.
(1)求 ,
, 的值;
的值;
(2)求证: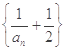 是等比数列,并求
是等比数列,并求 的通项公式
的通项公式 ;
;
(3)数列 满足
满足 ,数列
,数列 的前n项和为
的前n项和为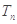 ,若不等式
,若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1) (2)
(2) (3)
(3)
解析试题分析:(1)分别令 代入
代入 ,即可求出
,即可求出 ,
, 的值
的值
(2)根据需要求证的结果,由 构造数列
构造数列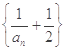 ,可得
,可得 (3)由(2)
(3)由(2) ,利用错位相减法求得
,利用错位相减法求得 ,分类讨论当n为偶数和n为奇数时 的情况,可求
,分类讨论当n为偶数和n为奇数时 的情况,可求 的取值范围
的取值范围
(1)由 知,
知, ,
,
又 是以
是以 为首项,
为首项, 为公比的等比数列,
为公比的等比数列, 
(2) ,
, 
 ,
,
两式相减得 ,
,

若n为偶数,则
若n为奇数,则

考点:等比数列,错位相减法求和,分类讨论思想

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 成等比数列,则圆锥曲线
成等比数列,则圆锥曲线 的离心率为
的离心率为  的首项
的首项 .
. 是等比数列,并求出
是等比数列,并求出 ;
; .
. 的首项
的首项 ,且
,且
 .
. 的前
的前 项和
项和 .
. 的前
的前 项和
项和 .
. ,都有
,都有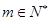 ,使得
,使得 成等比数列.
成等比数列. 中,已知
中,已知 ,
, ,
, .
.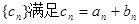 ,求
,求 的前
的前 项和
项和 .
. }中,
}中,
 }是等比数列,并求出数列{
}是等比数列,并求出数列{ 的前n项的和为
的前n项的和为 ,且
,且 ,
,
 是等比数列
是等比数列 与前n项的和
与前n项的和 若集合M=
若集合M= 恰有4个元素,求实数
恰有4个元素,求实数 的取值范围.
的取值范围.