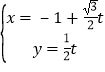题目内容
【题目】数列![]()
满足:![]() 或1(k=1,2,…,n-1).
或1(k=1,2,…,n-1).
对任意i,j,都存在s,t,使得![]() ,其中i,j,s,t∈{1,2,…,n}且两两不相等.
,其中i,j,s,t∈{1,2,…,n}且两两不相等.
(I)若m=2,写出下列三个数列中所有符合题目条件的数列的序号;
①1,1,1,2,2,2; ②1,1,1,1,2,2,2,2; ③1,1,1,1,1,2,2,2,2
(II)记![]() .若m=3,求S的最小值;
.若m=3,求S的最小值;
(III)若m=2018,求n的最小值.
【答案】(Ⅰ)②③;(Ⅱ)见解析;(Ⅲ)2026.
【解析】分析:(Ⅰ)分别把所给的三个数列代入题目条件中进行验证后可得出结果.(Ⅱ)当m=3时,设数列An中1,2,3出现频数依次为![]() ,由题意
,由题意![]() .假设
.假设![]() ,则与已知矛盾,从而
,则与已知矛盾,从而![]() ,同理可证
,同理可证![]() .假设
.假设![]() ,则与已知矛盾,所以
,则与已知矛盾,所以![]() ,由此能证明
,由此能证明![]() .(Ⅲ)设1,2,…,2018出现频数依次为
.(Ⅲ)设1,2,…,2018出现频数依次为![]() ,可得
,可得![]() ,则
,则![]() .取
.取![]() ,
,![]() ,得到的数列为:
,得到的数列为:![]()
![]() ,由此能出n的最小值.
,由此能出n的最小值.
详解:(I)数列![]() 满足:
满足:![]() 或1(k=1,2,…,n-1).对任意i,j,都存在s,t,使得
或1(k=1,2,…,n-1).对任意i,j,都存在s,t,使得![]() ,其中i,j,s,t∈{1,2,…,n}且两两不相等.
,其中i,j,s,t∈{1,2,…,n}且两两不相等.
∴在①中,1,1,1,2,2,2,不符合题目条件;
在②中,1,1,1,1,2,2,2,2,符合题目条件;
在③中,1,1,1,1,1,2,2,2,2,符合题目条件.
故所有符合题目条件的数列的序号为②③.
(II)当m=3时,设数列![]() 中1,2,3,出现频数依次为
中1,2,3,出现频数依次为![]() ,由题意
,由题意![]() .
.
①假设![]() ,则有
,则有![]() (对任意
(对任意![]() ),
),
与已知矛盾,所以![]() .
.
同理可证:![]() .
.
②假设![]() ,则存在唯一的
,则存在唯一的![]() ,使得
,使得![]() .
.
则对![]() ,有
,有![]() (k,s,t两两不相等),与已知矛盾,
(k,s,t两两不相等),与已知矛盾,
所以![]() .
.
综上![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
故S的最小值为20.
(III)设1,2,…,2018出现频数依次为![]() .
.
同(II)的证明,可得![]() ,
,
所以![]() .
.
取![]() ,
,![]() ,得到的数列为:
,得到的数列为:
![]()
下面证明![]() 满足题目要求.
满足题目要求.
对![]() ,不妨令
,不妨令![]() ,
,
①如果![]() 或
或![]() ,由于
,由于![]() ,所以符合条件;
,所以符合条件;
②如果![]() 或
或![]() ,
,
由于![]() ,
,![]() ,
,
所以也成立;
③如果![]() ,则可选取
,则可选取![]() ;同样的,如果
;同样的,如果![]() ,则可选取
,则可选取![]() ,使得
,使得![]() ,且i,j,s,t两两不相等;
,且i,j,s,t两两不相等;
④如果![]() ,则可选取
,则可选取![]() ,注意到这种情况每个数最多被选取了一次,因此也成立.
,注意到这种情况每个数最多被选取了一次,因此也成立.
综上对任意i,j,总存在s,t,使得![]() ,其中i,j,s,t∈{1,2,…,n}且两两不相等.
,其中i,j,s,t∈{1,2,…,n}且两两不相等.
因此![]() 满足题目要求,
满足题目要求,
所以n的最小值为2026.