题目内容

讨论函数

f（x）=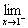

（1）求当x→1时的极限；

（2）求当x→2时的极限.

解：（1）∵f（x）=（x2+2x－2）=1，f（x）=x=1，

∴f（x）=f（x）=1.

∴f（x）=1.

（2）f（x）=x=2，

f（x）=（2x－4）=0，

∴f（x）≠f（x）.

∴f（x）在x=2点的极限不存在.

点评：分段函数在转折点处求极限，需研究这一点的左、右极限，只有它们相等时，才能说这一函数在该点有极限，其极限等于左、右极限.

练习册系列答案
相关题目
已知函数f（x）=lnx-ax-3（a≠0），
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）若对于任意的a∈[1，2]，若函数g(x)=x3+
x2
2
[m-2f′(x)]在区间（a，3）上有最值，求实数m的取值范围；
（Ⅲ）求证：ln(
1
22
+1)+ln(
1
32
+1)+ln(
1
42
+1)+…+ln(
1
n2
+1)＜1(n≥2，n∈N*)．
已知函数f(x)=
32
x2+2ax-a2lnx，二次函数g（x）=ax2-2x+1．
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）若-（a12+a22）=a1a23+a2a13-2a12a22=a1a2（a1-a2）2与g（x）在区间（a，a+2）内均为单调函数，求实数a的取值范围．
设函数f(x)=ax-
bx
，曲线y=f（x）在点（2，f（2））处的切线方程为7x-4y-12=0．
（1）求f（x）的解析式；
（2）讨论函数f（x）的单调性．
已知函数f（x）=lnx-x2+x+2
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若a＞0，求f（x）在区间（0，a]上的最大值；
（III）设函数g（x）=x3-（1+2e）x2+（m+1）x+2，（m∈R），试讨论函数f（x）与g（x）图象交点的个数．
已知函数f（x）=ax+x2-xlna（a＞1）．
（Ⅰ）试讨论函数f（x）的单调性；
（Ⅱ）若函数y=|f（x）-t|-1有三个零点，试求t的值；
（Ⅲ）若存在x1，x2∈[-1，1]，使得|f（x1）-f（x2）|≥e-1，试求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网