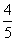题目内容
设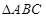 的三个内角分别为
的三个内角分别为 .向量
.向量 共线.
共线.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)设角 的对边分别是
的对边分别是 ,且满足
,且满足 ,试判断
,试判断
 的形状.
的形状.
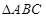 的三个内角分别为
的三个内角分别为 .向量
.向量 共线.
共线.(Ⅰ)求角
 的大小;
的大小;(Ⅱ)设角
 的对边分别是
的对边分别是 ,且满足
,且满足 ,试判断
,试判断
 的形状.
的形状.(Ⅰ)C= ;(Ⅱ)△
;(Ⅱ)△ 为等边三角形
为等边三角形
 ;(Ⅱ)△
;(Ⅱ)△ 为等边三角形
为等边三角形试题分析:(Ⅰ)∵
 与
与 共线,∴
共线,∴ 
 3分
3分 ∴C=
∴C= 6分
6分(Ⅱ)由已知
 根据余弦定理可得:
根据余弦定理可得: 8分
8分联立解得:


 ,所以△
,所以△ 为等边三角形, 12分
为等边三角形, 12分点评:三角形的形状的判定常常通过正弦定理和余弦定理,将已知条件中的边角关系转化为纯边或纯角的关系,寻找边之间的关系或角之间关系来判定.一般的,利用正弦定理的公式
 ,
, ,
, ,可将边转化为角的三角函数关系,然后利用三角函数恒等式进行化简,其中往往用到三角形内角和定理:
,可将边转化为角的三角函数关系,然后利用三角函数恒等式进行化简,其中往往用到三角形内角和定理: ;利用余弦定理公式
;利用余弦定理公式 ,
, ,
, ,可将有关三角形中的角的余弦转化为边的关系,然后充分利用代数知识来解决问题.
,可将有关三角形中的角的余弦转化为边的关系,然后充分利用代数知识来解决问题.
练习册系列答案
相关题目

 ,求
,求 的最大值和最小值;
的最大值和最小值; ,求
,求 的值.
的值. ,使等式
,使等式 成立;②函数
成立;②函数 有无数个零点;③函数
有无数个零点;③函数 是偶函数;④方程
是偶函数;④方程 的解集是
的解集是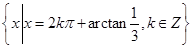 ;⑤把函数
;⑤把函数 的图像沿
的图像沿 轴方向向左平移
轴方向向左平移 个单位后,得到的函数解析式可以 表示成
个单位后,得到的函数解析式可以 表示成 ;⑥在同一坐标系中,函数
;⑥在同一坐标系中,函数 的图像和函数
的图像和函数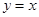 的图像只有1个公共点.
的图像只有1个公共点. .
.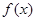 的最小值,并求使
的最小值,并求使 的集合;
的集合; 的图像可由
的图像可由 的图象经过怎样的变化得到.
的图象经过怎样的变化得到. 为锐角,且
为锐角,且 ,则
,则 的值是________.
的值是________.  ),其中ω>0,|
),其中ω>0,| ,若cos
,若cos cos
cos sin
sin .
. .
. 的最小正周期及其单调增区间:
的最小正周期及其单调增区间: 时,求
时,求 ,则
,则