题目内容
已知a为实数,数列{an}满足a1=a,当n≥2时,an=
,
(Ⅰ)当a=100,时,求数列{an}的前100项的和S100;
(Ⅱ)证明:对于数列{an},一定存在k∈N*,使0<ak≤3;
(Ⅲ)令bn=
,当2<a<3时,求证:
bi<
.
|
(Ⅰ)当a=100,时,求数列{an}的前100项的和S100;
(Ⅱ)证明:对于数列{an},一定存在k∈N*,使0<ak≤3;
(Ⅲ)令bn=
| an |
| 2n-(-1)n |
| n |
 |
| i=1 |
| 20+a |
| 12 |
分析:(Ⅰ)当a=100时,由题意知数列{an}的前34项成首项为100,公差为-3的等差数列,从第35项开始,奇数项均为3,偶数项均为1,由此能求出S100.
(Ⅱ)当0<a1≤3时,题意成立.当a1>3时,an=a1-3(n-1).设a1∈(3k,3k+3],(k≥1,k∈N*),则当n=k+1时,ak+1=a1-3k∈(0,3].命题成立.当a1≤0时,a2=4-a1>3,命题成立.由此能够证明原命题成立.
(Ⅲ)当2<a<3时,由an=
,知bn=
=
.因为bn>0,所以只要证明当n≥3时不等式成立即可.由此能够证明
bi<
bi<
.
(Ⅱ)当0<a1≤3时,题意成立.当a1>3时,an=a1-3(n-1).设a1∈(3k,3k+3],(k≥1,k∈N*),则当n=k+1时,ak+1=a1-3k∈(0,3].命题成立.当a1≤0时,a2=4-a1>3,命题成立.由此能够证明原命题成立.
(Ⅲ)当2<a<3时,由an=
|
|
| an |
| 2n-(-1)n |
|
| 2k-1 |
 |
| i=1 |
| 2k |
 |
| i=1 |
| 20+a |
| 12 |
解答:解:(Ⅰ)a=100时,
∵a1=100,当n≥2时,an=
,
∵a1=100,a2=97,…,a33=4,a34=1,a35=3,a36=1,a37=3,…,a100=1,
∴a=100时,
数列{an}的前34项成首项为100,公差为-3的等差数列,
从第35项开始,奇数项均为3,偶数项均为1,
从而S100=
+
…(3分)
=
+(3+1)×
=1717+132=1849.…(5分)
(Ⅱ)证明:①若0<a1≤3,则题意成立…(6分)
②若a1>3,此时数列{an}的前若干项满足an-an-1=3,
即an=a1-3(n-1).
设a1∈(3k,3k+3],(k≥1,k∈N*),
则当n=k+1时,ak+1=a1-3k∈(0,3].
从而此时命题成立…(8分)
③若a1≤0,由题意得a2=4-a1>3,
则由②的结论知此时命题也成立.
综上所述,原命题成立…(10分)
(Ⅲ)当2<a<3时,
因为an=
,
所以bn=
=
.…(11分)
因为bn>0,
所以只要证明当n≥3时不等式成立即可.
而b2k-1+b2k=
+
=
<
<
=
…(13分)
①当n=2k(k∈N*,且k≥2)时,
bi=b1+b2+
bi<
+
+(
+
+…+
)
=
+(a+4)×
=
+
<
+
=
.…(15分)
②当n=2k-1(k∈N*且k≥2)时,
由于bn>0,所以
bi<
bi<
.
综上所述,原不等式成立…(16分)
∵a1=100,当n≥2时,an=
|
∵a1=100,a2=97,…,a33=4,a34=1,a35=3,a36=1,a37=3,…,a100=1,
∴a=100时,
数列{an}的前34项成首项为100,公差为-3的等差数列,
从第35项开始,奇数项均为3,偶数项均为1,
从而S100=
| (100+97+94+…+4+1) |
| 共34项 |
| (3+1+…+3+1) |
| 共66项 |
=
| (100+1)×34 |
| 2 |
| 66 |
| 2 |
(Ⅱ)证明:①若0<a1≤3,则题意成立…(6分)
②若a1>3,此时数列{an}的前若干项满足an-an-1=3,
即an=a1-3(n-1).
设a1∈(3k,3k+3],(k≥1,k∈N*),
则当n=k+1时,ak+1=a1-3k∈(0,3].
从而此时命题成立…(8分)
③若a1≤0,由题意得a2=4-a1>3,
则由②的结论知此时命题也成立.
综上所述,原命题成立…(10分)
(Ⅲ)当2<a<3时,
因为an=
|
|
所以bn=
| an |
| 2n-(-1)n |
|
因为bn>0,
所以只要证明当n≥3时不等式成立即可.
而b2k-1+b2k=
| a |
| 22k-1+1 |
| 4-a |
| 22k-1 |
| a•22k-1+22k+1+(4-2a) |
| (22k-1+1)(22k-1) |
| a•22k-1+22k+1 |
| 24k-1+22k-1-1 |
| a•22k-1+22k+1 |
| 24k-1 |
| a+4 |
| 22k |
①当n=2k(k∈N*,且k≥2)时,
| 2k |
 |
| i=1 |
| 2k |
 |
| i=3 |
| a |
| 3 |
| 4-a |
| 3 |
| a+4 |
| 22×2 |
| a+4 |
| 22×3 |
| a+4 |
| 22×k |
=
| 4 |
| 3 |
| ||||
1-
|
=
| 4 |
| 3 |
(a+4)×(1-(
| ||
| 12 |
| 4 |
| 3 |
| a+4 |
| 12 |
=
| 20+a |
| 12 |
②当n=2k-1(k∈N*且k≥2)时,
由于bn>0,所以
| 2k-1 |
 |
| i=1 |
| 2k |
 |
| i=1 |
| 20+a |
| 12 |
综上所述,原不等式成立…(16分)
点评:本题考查数列与不等式的综合,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
 ,
,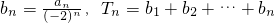 ,求证:当
,求证:当 时,
时,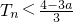 .
.