题目内容

△ABC中，
AB
•
BC
＜0，
BC
•
AC
＜0，则该三角形为（　　）
分析：由向量的定义与数量积的运算性质，
BC
•
AC
＜0即
CB
•
CA
＜0，得|
CB
|•|
CA
|cosC＜0，可得C为钝角，该三角形为钝角三角形．
解答：解：∵
BC
=-
CB
，
AC
=-
CA
，
∴
BC
•
AC
＜0，即（-
CB
）•（-
CA
）＜0
可得
CB
•
CA
＜0，得|
CB
|•|
CA
|cosC＜0
因此cosC＜0，结合C∈（0，π）得C为钝角
∴△ABC是钝角三角形
故选：C
点评：本题给出三角形中向量数量积的符号，求三角形的形状，着重考查了平面向量数量积的定义与运算性质、三角形状的判断等知识，属于基础题．
练习册系列答案
相关题目
如图，在Rt△ABC中，AB=BC=4，点E、F分别在线段AB、AC上，且EF∥BC，将△AEF沿EF折起到△PEF的位置，使得二面角P-EF-B的大小为60°．
（1）求证：EF⊥PB；
（2）当点E为线段AB的中点时，求PC与平面BCFE所成角的大小．
精英家教网
在△ABC中，AB=2，BC=3，∠ABC=
2
3
π，若使△ABC绕直线BC旋转一周，则所形成的几何体的体积是（　　）
A、6πB、5πC、4πD、3π
在△ABC中，
AB
=
c
，
AC
=
b
，若点D满足：
BD
=
DC
，则
AD
=（　　）
如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．
（Ⅰ）求证：OD∥平面PAB；
（Ⅱ）当k=
1
2
时，求直线PA与平面PBC所成角的正弦值；
（Ⅲ）当k取何值时，O在平面PBC内的射影恰好为△PBC的重心？
（注：若△ABC的三点坐标分别为A（x1，y1，z1），B（x2，y2，z2），C（x3，y3，z3），则该三角形的重心坐标为：(
x1+x2+x3
3
，
y1+y2+y3
3
，
z1+z2+z3
3
)．）
（2011•西城区二模）在△ABC中，“
AB
•
BC
=0”是“△ABC为直角三角形”的（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

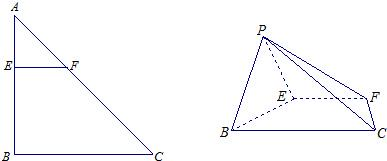
精英家教网