题目内容
已知矩形 的周长为
的周长为 ,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为 .
,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为 .


【解析】
试题分析:解法一:设正六棱柱的的底面边长为 ,高为
,高为 ,则
,则 ,所以
,所以 ,正六棱柱的体积
,正六棱柱的体积
 ,当且仅当
,当且仅当 时等号成立.此时
时等号成立.此时 .易知正六棱柱的外接球的球心是其上下中心连线的中点,如图所示,外接球的半径为
.易知正六棱柱的外接球的球心是其上下中心连线的中点,如图所示,外接球的半径为 所以外接球的表面积为
所以外接球的表面积为
解法二:设正六棱柱的的底面边长为 ,高为
,高为 ,则
,则 ,所以
,所以 ,正六棱柱的体积
,正六棱柱的体积 ,
, ,令
,令 ,解得
,解得 ,令
,令 得
得 ,即函数
,即函数 在
在 是增函数,在
是增函数,在 是减函数,所以
是减函数,所以 在
在 时取得最大值,此时
时取得最大值,此时 .易知正六棱柱的外接球的球心是其上下中心连线的中点,如图所示,外接球的半径为
.易知正六棱柱的外接球的球心是其上下中心连线的中点,如图所示,外接球的半径为 所以外接球的表面积为
所以外接球的表面积为

考点:1.几何体的表面积与体积;2.应用导数研究函数的最值;3.不等式选讲.

练习册系列答案
相关题目
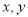 满足
满足 ,若
,若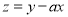
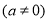 取得的最优解
取得的最优解 有无数个,则
有无数个,则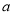 的值为( )
的值为( )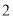 B.
B.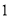 C.
C.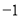
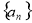 满足:存在正整数
满足:存在正整数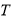 ,对于任意正整数
,对于任意正整数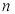 都有
都有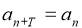 成立,则称数列
成立,则称数列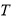 .已知数列
.已知数列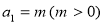 ,
, 则下列结论中错误的是( ).
则下列结论中错误的是( ).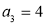 ,则
,则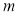 可以取3个不同的值;
可以取3个不同的值;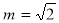 ,则数列
,则数列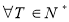 且
且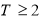 ,存在
,存在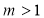 ,数列
,数列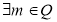 且
且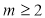 ,数列
,数列 为
为 ,那么输出的结果是( )
,那么输出的结果是( )
 B.
B.
 D.
D.
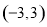 中任取两个整数
中任取两个整数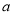 ,
,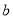 ,设点
,设点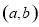 在圆
在圆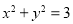 内的概率为
内的概率为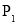 ,从区间
,从区间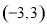 中任取两个实数
中任取两个实数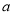 ,
,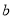 ,直线
,直线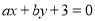 和圆
和圆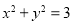 相离的概率为
相离的概率为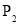 ,则( )
,则( )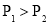 B.
B.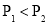
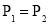 D.
D.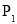 和
和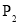 的大小关系无法确定
的大小关系无法确定 为
为 ,那么输出的结果是( )
,那么输出的结果是( )
 B.
B.
 D.
D.
 ,设集合
,设集合 ,
, ,则集合
,则集合 中元素的个数为( )
中元素的个数为( ) B.
B. C.
C. D.
D.
 满足
满足 ,则
,则 的最小值是( )
的最小值是( ) B.
B. C.
C. D.
D.

 B.
B. C.
C. D.
D.