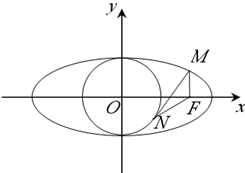
题目内容
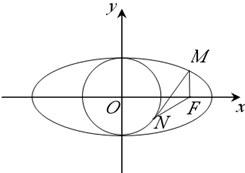 F为椭圆
F为椭圆| x2 |
| 5 |
分析:根据椭圆的性质,可求出F点坐标,进而结合已知中MF⊥x轴,求出M点坐标,根据直线MN与圆相切求出点N的坐标后,代入两点之间距离公式,可得答案.
解答:解:∵F为椭圆
+y2=1的右焦点,
∴F点的坐标为(2,0)
∵MF⊥x轴,M在椭圆上且在第一象限
∴M点的坐标为(2,
)
设直线MN的斜率为k(k>0)
则直线MN的方程为y-
=k(x-2)
即kx-y-2k+
=0
∵直线MN与圆x2+y2=1相切
∴原点(圆心)到直线MN的距离等于半径1,
即
=1
解得k=
,或k=-
(舍去)
∴直线MN的方程为
x-y-
=0…①
联立圆方程x2+y2=1可得
N点坐标为(
,
)
∴|NF|=
=
故选A
| x2 |
| 5 |
∴F点的坐标为(2,0)
∵MF⊥x轴,M在椭圆上且在第一象限
∴M点的坐标为(2,
| ||
| 5 |
设直线MN的斜率为k(k>0)
则直线MN的方程为y-
| ||
| 5 |
即kx-y-2k+
| ||
| 5 |
∵直线MN与圆x2+y2=1相切
∴原点(圆心)到直线MN的距离等于半径1,
即
|-2k+
| ||||
|
解得k=
2
| ||
| 5 |
2
| ||
| 15 |
∴直线MN的方程为
2
| ||
| 5 |
3
| ||
| 5 |
联立圆方程x2+y2=1可得
N点坐标为(
| 2 |
| 3 |
| ||
| 3 |
∴|NF|=
(2-
|
| ||
| 3 |
故选A
点评:本题考查的知识点是椭圆的简单性质,直线与圆的位置关系,两点之间的距离,其中求出N点坐标是解答的关键.

练习册系列答案
相关题目
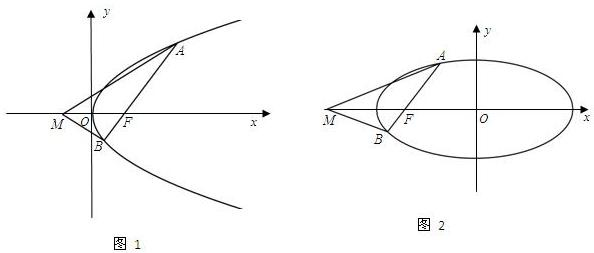
 轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.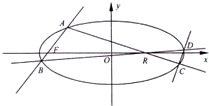 如图,椭圆E:
如图,椭圆E: