题目内容
2.已知二面角α-l-β,空间中有一点A,且AC⊥α于C,AB⊥β于B,若∠BAC=75°,则二面角α-l-β的大小为75°或105°.分析 画出图形,判断∠BAC=75°与二面角α-l-β的大小关系,求解即可.
解答 解:如图,过AC与AB做平面,与平面αβ的交线为:BO,CO,AC⊥α于C,AB⊥β于B,可得 l⊥平面ABC,
∠BOC就是二面角α-l-β的大小,在图形1中,∠BOC=180°-75°=105°.
在图形2中,∠BOC=75°.
故答案为:75°或105°.
点评 本题考查二面角的平面角的求法,考查计算能力,空间想象能力,是易错题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.若f(x)=-x2+2ax与g(x)=$\frac{a}{x+1}$在区间(1,+∞)上都是减函数,则a的取值范围是( )
| A. | (-1,0)∪(0,1) | B. | (-1,0)∪(0,1] | C. | (0,1) | D. | (0,1] |
17.下列说法中,正确的是( )
| A. | 数据5,4,4,3,5,2的众数是4 | |
| B. | 根据样本估计总体,其误差与所选择的样本容量无关 | |
| C. | 数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半 | |
| D. | 频率分布直方图中各小长方形的面积等于相应各组的频数 |
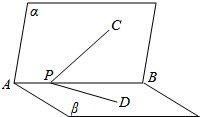 如图,平面α⊥平面β,平面α∩平面β=AB,P∈AB,C∈α,D∈β,且∠CPB=∠DPB=45°,则∠CPD=60°.
如图,平面α⊥平面β,平面α∩平面β=AB,P∈AB,C∈α,D∈β,且∠CPB=∠DPB=45°,则∠CPD=60°.