Question

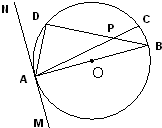（几何证明选讲）如图，半径是3

3

的⊙O中，AB是直径，MN是过点A的⊙O的切线，AC，BD相交于点P，且∠DAN=30°，CP=2，PA=9，又PD＞PB，则线段PD的长为

6

．

Answer 1

分析：根据MN切圆O与A点，得到弦切角∠DAN=∠B=30°，再用直径AB得到直角三角形ADB，计算出BD长等于9，最后利用相交弦定理得到PB•PD=PC•PA=18，从而得到线段PD的长．

解答：解：∵AB是⊙O的直径，
∴AD⊥DB
又∵直线MN与圆O相切于点A
∴∠B=∠DAN=30°
∴Rt△ADB中，AD=

1

2

AB=3

3

，BD=

3

2

AB=9
∵⊙O的弦AC、BD交于P点
∴PA•PC=PB•PD
设PD长为x，得2×9=x（9-x）
解之，得x=3或6
∵PD＞PB
∴x=6
故答案为6

点评：本题考查了弦切角、与圆有关的比例线段的相关知识，属于中档题．解题时应该充分利用直径AB这个条件，化难为易．