Question

已知f（x）=log₂ （-1＜x＜1）．
（1）若f（a）+f（b）=0，求证：a+b=0；
（2）设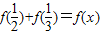，求x的值；
（3）设x₁、x₂∈（-1，1），是否存在x₃∈（-1，1），使得f（x₁）+f（x₂）=f（x₃），若存在，求出x₃，并证明你的结论；若不存在，请说明理由．

Answer 1

【答案】分析：（1）利用对数的性质通过f（a）+f（b）=0，化简即可得到a+b=0；
（2）通过化简方程，，即可直接求出x的值；
（3）通过f（x₁）+f（x₂）=f（x₃），直接求出x₃，然后利用分析法证明结论．
解答：解：（1）证明：由f（a）+f（b）=0得，
，∴（1-a）（1-b）=（1+a）（1+b），化简得a+b=0．…（4分）
（2）解：，，，
由得，解得．…（8分）
（3）解：假设存在x₃∈（-1，1）使得f（x₁）+f（x₂）=f（x₃），…（9分）
∵，，
∴，解得，…（12分）
下证，
先用分析法证明，∵x₁、x₂∈（-1，1），∴1+x₁x₂＞0．
要证明，即要证x₁+x₂＜1+x₁x₂，即要证（1-x₁）（1-x₂）＞0，
∵x₁、x₂∈（-1，1），∴1+x₁＞0，1+x₂＞0，（1-x₁）（1-x₂）＞0，
同理可证，…（15分）
所以存在，使得f（x₁）+f（x₂）=f（x₃）．…（16分）
点评：本题考查函数与方程的综合应用，分析法证明问题的方法，考查分析问题解决问题的能力．