题目内容
甲、乙、丙三人进行乒乓球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为 ,各局比赛的结果相互独立,第1局甲当裁判.
,各局比赛的结果相互独立,第1局甲当裁判.
(1)求第4局甲当裁判的概率;
(2)用X表示前4局中乙当裁判的次数,求X的分布列和数学期望.
(1)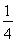 (2)
(2)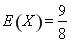
【解析】
试题分析:(1)根据题意,甲第一局当裁判,则第二局一定是参加比赛,第四局当裁判,说明第三局继续参加比赛,所以,甲参加了第二、三两局的比赛,且第二局胜,第三局负.
(2)根据题意,在四局比赛中,乙参赛的情况与比赛结果可用下表表示五种情况:
| 第一局 | 第二局 | 第三局 | 第四局 | 当裁判次数 |
1 | 参赛(胜) | 参赛(胜) | 参赛(胜) | 参赛 | 0 |
2 | 参赛(胜) | 参赛(胜) | 参赛(负) | 裁判 | 1 |
3 | 参赛(胜) | 参赛(负) | 裁判 | 参赛 | 1 |
4 | 参赛(负) | 裁判 | 参赛(胜) | 参赛 | 1 |
5 | 参赛(负) | 裁判 | 参赛(负) | 裁判 | 2 |
由此明确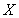 的所有可能的值,以及对应每个取值的含义,求出
的所有可能的值,以及对应每个取值的含义,求出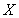 的分布列,进而求出
的分布列,进而求出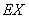 的值.
的值.
试题解析:(1)记A1表示事件“第2局结果为甲胜”,
A2表示事件“第3局甲参加比赛时,结果为甲负”,
A表示事件“第4局甲当裁判”.
则A=A1·A2.
P(A)=P(A1·A2)=P(A1)P(A2)=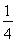 . 4分
. 4分
(2)X的可能取值为0,1,2.
记A3表示事件“第3局乙和丙比赛时,结果为乙胜丙”,
B1表示事件“第1局结果为乙胜丙”,
B2表示事件“第2局乙和甲比赛时,结果为乙胜甲”,
B3表示事件“第3局乙参加比赛时,结果为乙负”.
则P(X=0)=P(B1·B2·A3)=P(B1)P(B2)P(A3)=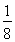 ,
,
P(X=2)=P(B1·B3)=P(B1)P(B3)= ,
,
P(X=1)=1-P(X=0)-P(X=2)=1-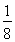 -
-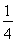 =
=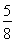 .
.
∴X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
∴E(X)=0×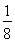 +1×
+1×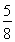 +2×
+2×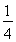 =
=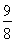 . 12分
. 12分
考点:1、独立重复试验.2、离散型随机变量的分布列与数学期望.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案

