题目内容
甲,乙,丙三人进行某项比赛,设某一局中三个人取胜的概率相等,比赛规定先胜三局者为整场比赛的优胜者,若甲胜了第一,三局,乙胜了第二局,问丙成为整场比赛优胜者的概率是多少?分析:由题意可得,每个人在一局中获胜的概率都是
,欲丙成为整场比赛的优胜者,则需在未来的三次中,丙获胜三次;或在前三次中,丙获胜两次乙胜一次,而第四次为丙获胜,即可得答案.
| 1 |
| 3 |
解答:解:设A,B,C分别表示每局比赛中甲,乙,丙获胜的事件,则P(A)=P(B)=P(C)=
.
欲丙成为整场比赛的优胜者,则需在未来的三次中,丙获胜三次;或在前三次中,丙获胜两次乙胜一次,
而第四次为丙获胜.故本题欲求的概率为p=
(
)3(
)0(
)0+
(
)2(
)(
)0=
.
| 1 |
| 3 |
欲丙成为整场比赛的优胜者,则需在未来的三次中,丙获胜三次;或在前三次中,丙获胜两次乙胜一次,
而第四次为丙获胜.故本题欲求的概率为p=
| 3! |
| 3! 0! 0! |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3! |
| 2! 1! 0! |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 27 |
点评:本题考查等可能事件的概率,体现了分类讨论的数学思想,判断“欲丙成为整场比赛的优胜者,则需在未来的三次中,丙获胜三次;或在前三次中,丙获胜两次乙胜一次,而第四次为丙获胜.”是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
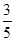 ,甲胜丙的概
,甲胜丙的概 ,乙胜丙的概率为
,乙胜丙的概率为 网]
网] ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 、
、 ,且甲、乙投篮是否命中互不影响.
,且甲、乙投篮是否命中互不影响.