题目内容
如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是底面边长的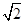 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.
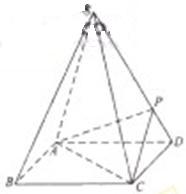
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,则侧棱SC上是否存在一点E,使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由.
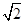 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,则侧棱SC上是否存在一点E,使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由.
(Ⅰ)只需证明 ;(Ⅱ)只需使得平面
;(Ⅱ)只需使得平面
 ;(Ⅱ)只需使得平面
;(Ⅱ)只需使得平面
试题分析:解:(Ⅰ)连BD,设AC交BD于O,由题意
 。在正方形ABCD中,
。在正方形ABCD中, ,所以
,所以 ,得
,得 .………………4分
.………………4分(Ⅱ) 在棱SC上存在一点E,使

设正方形边长
 ,则
,则 。
。又
 ,所以
,所以 ,
,连
 , 由
, 由 ,知
,知 ,所以
,所以 ,
,则
 ,故可在
,故可在 上取一点
上取一点 ,使
,使 ,过
,过 作
作 的平行线与
的平行线与 的交点即为
的交点即为 ,连BN。
,连BN。在
 中知
中知 ,又由于
,又由于 ,故平面
,故平面 ,得
,得 ,由于
,由于 ,故
,故 .………………12分
.………………12分点评:结合定理可解决此题。但第二小题属于讨论题目,相对较难。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
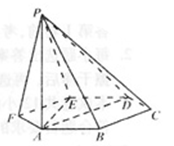
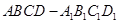 是正方体,其中
是正方体,其中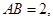

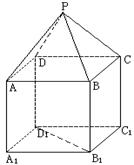
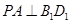 ;
;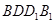 所成的锐二面角
所成的锐二面角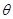 的余弦值;
的余弦值;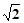 ,D是A1B1中点.
,D是A1B1中点.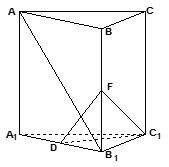
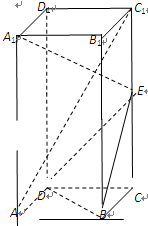
 为底面的直棱柱被平面
为底面的直棱柱被平面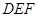 所截而得.
所截而得. 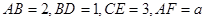 ,
, 为
为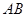 的中点.
的中点.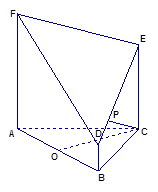
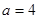 时,求平面
时,求平面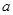 为何值时,在棱
为何值时,在棱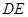 上存在点
上存在点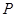 ,使
,使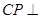 平面
平面