题目内容
在平面内有DABC和点O,若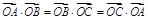 ,则点O是DABC的( )
,则点O是DABC的( )
| A.重心 | B.垂心 | C.内心 | D.外心 |
B
解析试题分析:∵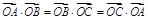 ∴
∴ ;
;
∴ =0,∴OB⊥AC,
=0,∴OB⊥AC,
同理可得OA⊥BC,∴点O是△ABC的三条高的交点,故选B。
考点:平面向量的数量积,向量垂直的条件。
点评:简单题,两向量垂直,它们的数量积为0.

 阶梯计算系列答案
阶梯计算系列答案已知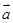 、
、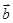 是平面向量,若
是平面向量,若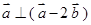 ,
,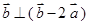 ,则
,则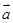 与
与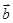 的夹角是( )
的夹角是( )
A.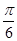 | B.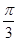 | C.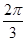 | D.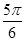 |
已知向量 ,
, 满足|
满足| |="2," |
|="2," |  |=l,且(
|=l,且( +
+ )⊥(
)⊥(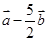 ),则
),则 与
与 的夹角为
的夹角为
A.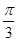 | B.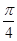 | C.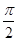 | D.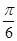 |
平面向量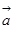 与
与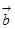 的夹角为
的夹角为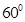 ,
,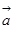 =(2,0),
=(2,0),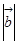 ="1" 则
="1" 则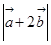 =( )
=( )
A. | B.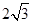 | C.4 | D.12 |
若向量 满足
满足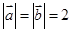 ,且
,且 ,则向量
,则向量 的夹角为
的夹角为
| A.30° | B.45° | C.60° | D.120° |
已知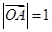 ,
,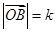 ,
,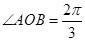 ,点C在
,点C在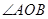 内,
内, 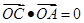 ,若
,若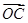 =2m
=2m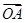 +m
+m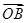 (
(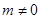 ),则
),则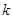 =( )
=( )
| A.1 | B.2 | C.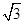 | D.4 |
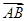 ·
·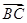 =3,△ABC的面积S∈[
=3,△ABC的面积S∈[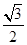 ,
, ],则
],则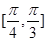
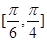
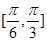
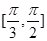
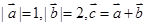 ,且
,且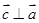 ,则向量
,则向量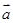 与
与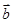 的夹角为( )
的夹角为( )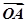 =
=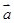 ,
,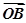 =
=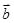 ,其中
,其中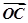 =λ
=λ