题目内容
在△ABC中,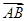 ·
·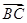 =3,△ABC的面积S∈[
=3,△ABC的面积S∈[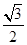 ,
, ],则
],则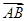 与
与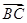 夹角的取值范围是( )
夹角的取值范围是( )
A.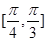 | B.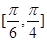 | C.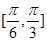 | D.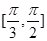 |
B
解析试题分析:利用向量的数量积求得表达式,根据三角形面积的范围,可以得到B的范围,然后求题目所求夹角的取值范围.根据题意,由于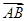 ·
·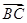 =3=-
=3=- ,故可知tanB的范围是
,故可知tanB的范围是 那么可知π-B∈
那么可知π-B∈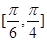 ,故答案可知为B.
,故答案可知为B.
考点:平面向量数量积的运算
点评:本题考查平面向量数量积的运算,数量积表示两个向量的夹角,考查计算能力,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知A=(1,-2),若向量 与a=(2,-3)反向,|
与a=(2,-3)反向,| |=4
|=4 ,则点B的坐标为( )
,则点B的坐标为( )
| A.(10,7) | B.(-10,7) | C.(7,-10) | D.(-7,10) |
若向量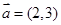 ,
,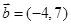 ,则
,则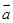 在
在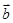 方向上的投影为( )
方向上的投影为( )
A.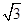 | B.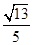 | C.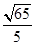 | D.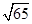 |
已知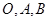 是平面上的三个点,直线
是平面上的三个点,直线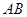 上有一点
上有一点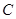 满足
满足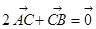 ,则
,则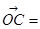 ( )
( )
A. | B. | C.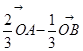 | D.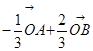 |
在平面内有DABC和点O,若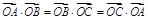 ,则点O是DABC的( )
,则点O是DABC的( )
| A.重心 | B.垂心 | C.内心 | D.外心 |
已知向量 ,则
,则 等于( )
等于( )
A. | B.3 | C.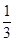 | D. |
若向量 和向量
和向量 平行,则
平行,则  ( )
( )
A. | B. | C. | D. |
若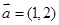 ,
, ,
, ,则
,则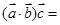
A. | B. | C. | D.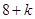  |
已知a,b是平面内两个互相垂直的单位向量,若向量c满足(a-c)·(b一c)=0,则|c|的最大值是
| A.1 | B. | C.2 | D. |