题目内容
已知过原点的动直线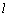 与圆
与圆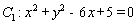 相交于不同的两点
相交于不同的两点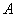 ,
,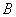 .
.
(1)求圆 的圆心坐标;
的圆心坐标;
(2)求线段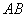 的中点
的中点 的轨迹
的轨迹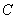 的方程;
的方程;
(3)是否存在实数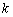 ,使得直线
,使得直线 与曲线
与曲线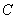 只有一个交点:若存在,求出
只有一个交点:若存在,求出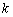 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【解析】(1)由 得
得 ,
,
∴ 圆 的圆心坐标为
的圆心坐标为 ;
;
(2)设 ,则
,则
∵ 点 为弦
为弦 中点即
中点即 ,
,
∴  即
即 ,
,
∴ 线段 的中点
的中点 的轨迹的方程为
的轨迹的方程为 ;
;
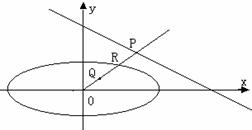
(3)由(2)知点 的轨迹是以
的轨迹是以 为圆心
为圆心 为半径的部分圆弧
为半径的部分圆弧 (如下图所示,不包括两端点),且
(如下图所示,不包括两端点),且 ,
, ,又
,又 直线
直线 :
: 过定点
过定点 ,
,

 [来源:Z+xx+k.Com]
[来源:Z+xx+k.Com]
当直线 与圆
与圆 相切时,由
相切时,由 得
得 ,又
,又 ,结合上图可知当
,结合上图可知当 时,直线
时,直线 :
: 与曲线
与曲线 只有一个交点.
只有一个交点.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 个不同的点两两距离都相等,则正整数
个不同的点两两距离都相等,则正整数 的直径,
的直径, ,
, 是圆
是圆 ,过圆心
,过圆心 的平行线,分别交
的平行线,分别交 于点
于点 和点
和点 ,则
,则

 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.

 元
元 B.
B. C.
C. D.
D.
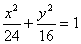 ,直线
,直线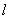 :
: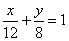 ,
,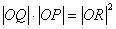 .当点P在
.当点P在