题目内容
已知函数 ,
,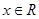 .求:
.求:
(I)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(II)求函数 在区间
在区间 上的值域.
上的值域.
(I) ,
, ;(II)
;(II) .
.
解析试题分析:(I)先由二倍角公式对 进行降次,然后利用公式
进行降次,然后利用公式 (其中
(其中 )将
)将 变成
变成 的形式,从而可以求出最小正周期和单调递增区间,在求单调区间时要特别注意
的形式,从而可以求出最小正周期和单调递增区间,在求单调区间时要特别注意 的正负,结合复合函数同增异减的规律,避免把单调增区间错求为单调减区间;(II)求函数
的正负,结合复合函数同增异减的规律,避免把单调增区间错求为单调减区间;(II)求函数 在区间
在区间 上的值域问题,先由
上的值域问题,先由 的范围即区间
的范围即区间 相位
相位 的范围,从而得到
的范围,从而得到 ,最后即得到
,最后即得到 的范围,也就是
的范围,也就是 的值域.
的值域.
试题解析:(I)由二倍角的正余弦公式及其变形,得


 4分
4分 函数
函数 的最小正周期
的最小正周期 , 6分
, 6分 即
即 时
时 为单调递增函数
为单调递增函数 的单调递增区间为
的单调递增区间为 8分
8分
(II)由题意得
 10分
10分 ,即
,即 ,
,
 的值域为
的值域为 12分
12分
考点:1.三角恒等变换;2.三角函数的基本运算;3.函数 的图像和性质.
的图像和性质.

练习册系列答案
相关题目
 (其中
(其中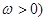 的最小正周期为
的最小正周期为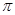 .
.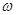 的值,并求函数
的值,并求函数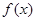 的单调递减区间;
的单调递减区间; 中,
中, 分别是角
分别是角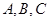 的对边,若
的对边,若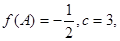
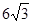 ,求
,求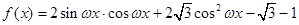 (其中
(其中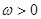 ),
),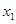 、
、 是函数
是函数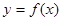 的两个不同的零点,且
的两个不同的零点,且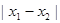 的最小值为
的最小值为 .
. 的值;
的值;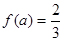 ,求
,求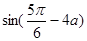 的值.
的值.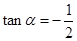 ,求
,求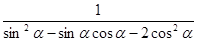 的值;
的值;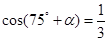 ,且
,且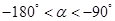 ,求
,求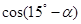 的值.
的值.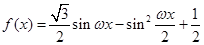 (
( )的最小正周期为
)的最小正周期为 .
.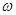 的值及函数
的值及函数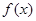 的单调递增区间;
的单调递增区间;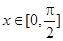 时,求函数
时,求函数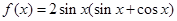 .
.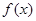 的最小正周期;
的最小正周期;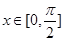 时,求
时,求 .
.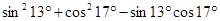 ;
;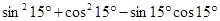 ;
; 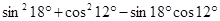 ;
;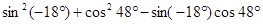 ;
;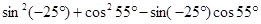 .
.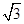 sinωxcosωx(ω>0)的最小正周期为π,
sinωxcosωx(ω>0)的最小正周期为π,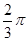 ]上的值域.
]上的值域.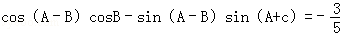 .
.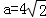 ,b=5,求向量
,b=5,求向量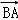 在
在 方向上的投影.
方向上的投影.