题目内容
7.已知命题p,q是简单命题,则“p∨q是真命题”是“¬p是假命题”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分有不必要条件 |
分析 由“¬p是假命题”可得:p是真命题,可得“p∨q是真命题”.反之不成立.
解答 解:由“¬p是假命题”可得:p是真命题,可得“p∨q是真命题”.
反之不成立,例如p是假命题,q是真命题.
∴“p∨q是真命题”是“¬p是假命题”的必要不充分条件.
故选:B.
点评 本题考查了复合命题真假的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
15.已知三棱锥O-ABC底面ABC的顶点在半径为$\sqrt{2}$的球O表面上,且AB=$\sqrt{2}$,AC=$\sqrt{2}$,BC=2,则三棱锥O-ABC的体积为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
2.设函数g(x)是R上的偶函数,当x<0时,g(x)=ln(1-x),函数$f(x)=\left\{\begin{array}{l}{x^3},x≤0\\ g(x),x>0\end{array}\right.$满足f(2-x2)>f(x),则实数x的取值范围是( )
| A. | (-∞,1)∪(2,+∞) | B. | (-∞,-2)∪(1,+∞) | C. | (1,2) | D. | (-2,1) |
19.已知向量$\overrightarrow a\;,\;\;\overrightarrow b$都是非零向量,“$\overrightarrow a•\overrightarrow b=|{\overrightarrow a}|•|{\overrightarrow b}|$”是“$\overrightarrow a∥\overrightarrow b$”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充分必要条件 | D. | 既非充分也非必要条件 |
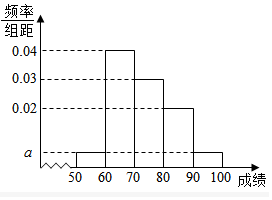 某小学1000名学生期中考试数学成绩的频率分布直方图如图所示.其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].根据统计学的知识估计成绩在[80,90)内的人数约为200.
某小学1000名学生期中考试数学成绩的频率分布直方图如图所示.其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].根据统计学的知识估计成绩在[80,90)内的人数约为200. 进位制是人们为了计数和运算方便而约定的记数系统,在日常生活中,我们最熟悉、最常用的是十进制.如图是实现将某进制数a化为十进制数b的程序框图,若输入的k=2,a=110,n=3,则输出的b=( )
进位制是人们为了计数和运算方便而约定的记数系统,在日常生活中,我们最熟悉、最常用的是十进制.如图是实现将某进制数a化为十进制数b的程序框图,若输入的k=2,a=110,n=3,则输出的b=( )