题目内容

在△OAB中，
OC
=
1
4
OA
，
OD
=
1
2
OB
，AD与BC交于点M，设
OA
=
a
，
OB
=
b
，以
a
、
b
为基底表示
OM
，则
OM
=
 
．
分析：由BMC三点共线，知
OM
=x
OC
+（1-x）
OB
=x•
a
4
+（1-x）•
b
；由AMD三点共线，知
OM
=y
OA
+（1-y）
OD
=y
a
+（1-y）•
b
2
，所以x=
4
7
，y=
1
7
，所以
OM
=
a
7
+
3
b
7
．
解答：解：∵BMC三点共线，
∴
OM
=x
OC
+（1-x）
OB
=x•
a
4
+（1-x）•
b
，
∵AMD三点共线，
∴
OM
=y
OA
+（1-y）
OD
=y
a
+（1-y）•
b
2
，
即
x
4
=y，且1-x=
1-y
2
，
所以 x=
4
7
，y=
1
7
，
所以
OM
=
a
7
+
3
b
7
．
故答案为：
a
7
+
3
b
7
．
点评：本题考查向量的线性运算性质和几何意义，解题时要认真审题，注意向量的几何意义的灵活运用．
练习册系列答案
相关题目
精英家教网如图，在△OAB中，
OC
=
1
3
OA
，
OD
=
1
2
OB
，AD与BC交于点M，
设
OA
=
a
，
OB
=
b
，
（1）试用向量
a
和
b
表示
OM
；
（2）在线段AC上取一点E，线段BD上取一点F，使EF过M点，
OE
=λ
OA
，
OF
=μ
OB
，求证：
1
λ
+
2
μ
=5．
如图所示，在△OAB中，OA＞OB，OC=OB，设
OA
=
a
，
OB
=
b
，若
AC
=λ•
AB
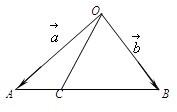
，则实数λ的值为（　　）精英家教网
A、
a
•(
a
-
b
)  
|
a
-
b
|
B、
a
•(
a
-
b
)  
|
a
-
b
|2
C、
a
2-
b
2
|
a
-
b
|
D、
a
2-
b
2
|
a
-
b
|2
在△OAB中，
（1）若C为直线AB上一点，且
AC
=λ
CB
(λ≠-1)，求证：
OC
=
OA
+λ
OB
1+λ
；
（2）若
OA
•
OB
=0，|
OA
|=|
OB
|=a，且C为线段AB上靠近A的一个三等分点，求
OC
•
AB
的值；
（3）若|
OA
|=1，|
OB
|=
3
，且P1，P2，P3，…，Pn-1为线段AB的n（n≥2）个等分点，求
OP1
•
AB
+
OP2
•
AB
+…+
OPn-1
•
AB
的值．
如图，在△OAB中，已知|
OA
|=2，|
OB
|=2
3
，∠AOB=90°，单位圆O与OA交于C，
AD
=λ
AB
，λ∈(0，1)，P为单位圆O上的动点．
（1）若
OD
=
3
4
OA
+
1
4
OB
，求λ的值；
（2）若
OC
+
OP
=
OD
，求
OC
•
OP
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

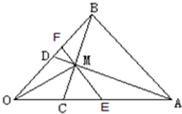精英家教网