题目内容
双曲线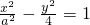 的左、右焦点分别为F1、F2,P是双曲线上一点,PF1的中点在y轴上,线段PF2的长为
的左、右焦点分别为F1、F2,P是双曲线上一点,PF1的中点在y轴上,线段PF2的长为 ,则该双曲线的离心率为
,则该双曲线的离心率为
- A.

- B.

- C.

- D.
D
分析:根据题意,得OQ是△PF1F2的中位线,得PF2⊥F1F2,Rt△PF1F2中算出|PF1|= +2a,|F1F2|=2c=2
+2a,|F1F2|=2c=2 ,利用勾股定理列出关于a的方程,解出a=3,从而c=
,利用勾股定理列出关于a的方程,解出a=3,从而c= =
= ,得到双曲线的离心率.
,得到双曲线的离心率.
解答: 解:∵PF1的中点Q在y轴上,O为F1F2的中点
解:∵PF1的中点Q在y轴上,O为F1F2的中点
∴OQ是△PF1F2的中位线,得OQ∥PF2,
由此可得PF2⊥F1F2,
根据双曲线的定义,得|PF1|=|PF2|+2a= +2a,
+2a,
而|F1F2|=2c=2
∴Rt△PF1F2中,|PF2|2+|F1F2|2=|PF1|2,
即 +4(a2+4)=(
+4(a2+4)=( +2a)2,解之得a=3
+2a)2,解之得a=3
∴c= =
= ,得双曲线的离心率e=
,得双曲线的离心率e= =
=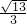
故选:D
点评:本题给出双曲线一条焦半径的中点恰好在y轴上,求双曲线的离心率,着重考查了双曲线的标准方程、基本概念和简单几何性质等知识,属于中档题.
分析:根据题意,得OQ是△PF1F2的中位线,得PF2⊥F1F2,Rt△PF1F2中算出|PF1|=
 +2a,|F1F2|=2c=2
+2a,|F1F2|=2c=2 ,利用勾股定理列出关于a的方程,解出a=3,从而c=
,利用勾股定理列出关于a的方程,解出a=3,从而c= =
= ,得到双曲线的离心率.
,得到双曲线的离心率.解答:
 解:∵PF1的中点Q在y轴上,O为F1F2的中点
解:∵PF1的中点Q在y轴上,O为F1F2的中点∴OQ是△PF1F2的中位线,得OQ∥PF2,
由此可得PF2⊥F1F2,
根据双曲线的定义,得|PF1|=|PF2|+2a=
 +2a,
+2a,而|F1F2|=2c=2

∴Rt△PF1F2中,|PF2|2+|F1F2|2=|PF1|2,
即
 +4(a2+4)=(
+4(a2+4)=( +2a)2,解之得a=3
+2a)2,解之得a=3∴c=
 =
= ,得双曲线的离心率e=
,得双曲线的离心率e= =
=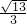
故选:D
点评:本题给出双曲线一条焦半径的中点恰好在y轴上,求双曲线的离心率,着重考查了双曲线的标准方程、基本概念和简单几何性质等知识,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 (2011•天津模拟)如图,椭圆
(2011•天津模拟)如图,椭圆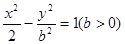 的左、右焦点分别是
的左、右焦点分别是 、
、 ,其一条渐近线方程为
,其一条渐近线方程为 ,点
,点 在双曲线上.则
在双曲线上.则 ·
· =
=