题目内容
二次函数f(x)=px2+qx+r中实数p、q、r满足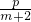 +
+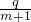 +
+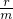 =0,其中m>0,求证:
=0,其中m>0,求证:
(1)pf( )<0;
)<0;
(2)方程f(x)=0在(0,1)内恒有解.
证明:(1)pf( )
)
=p[p( )2+q(
)2+q( )+r]
)+r]
=pm[ +
+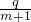 +
+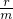 ]
]
=pm[ -
-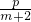 ]
]
=p2m[ ]
]
=p2m[- ].
].
由于f(x)是二次函数,故p≠0.
又m>0,所以pf( )<0.
)<0.
(2)由题意,得f(0)=r,f(1)=p+q+r.
①当p>0时,由(1)知f( )<0.
)<0.
若r>0,则f(0)>0,又f( )<0,
)<0,
∴f(x)=0在(0, )内有解;
)内有解;
若r≤0,则f(1)=p+q+r=p+(m+1)(-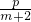 -
-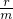 )+r=
)+r=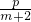 -
-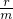 >0,
>0,
又f( )<0,
)<0,
所以f(x)=0在( ,1)内有解.
,1)内有解.
因此方程f(x)=0在(0,1)内恒有解.
②当p<0时,同样可以证得结论.
分析:(1)把x= 代入原函数,利用题设中p、q、r的关系进一步证明.
代入原函数,利用题设中p、q、r的关系进一步证明.
(2)先对p进行分类讨论,再对r进行分类讨论.
点评:(1)题目点明是“二次函数”,这就暗示着二次项系数p≠0,若将题中的“二次”两个字去掉,所证结论相应更改.
(2)对字母p、r分类时先对哪个分类是有一定讲究的.本题的证明中,先对p分类,然后对r分类显然是比较好的.
 )
)=p[p(
 )2+q(
)2+q( )+r]
)+r]=pm[
 +
+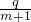 +
+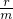 ]
]=pm[
 -
-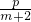 ]
]=p2m[
 ]
]=p2m[-
 ].
].由于f(x)是二次函数,故p≠0.
又m>0,所以pf(
 )<0.
)<0.(2)由题意,得f(0)=r,f(1)=p+q+r.
①当p>0时,由(1)知f(
 )<0.
)<0.若r>0,则f(0)>0,又f(
 )<0,
)<0,∴f(x)=0在(0,
 )内有解;
)内有解;若r≤0,则f(1)=p+q+r=p+(m+1)(-
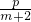 -
-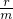 )+r=
)+r=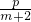 -
-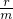 >0,
>0,又f(
 )<0,
)<0,所以f(x)=0在(
 ,1)内有解.
,1)内有解.因此方程f(x)=0在(0,1)内恒有解.
②当p<0时,同样可以证得结论.
分析:(1)把x=
 代入原函数,利用题设中p、q、r的关系进一步证明.
代入原函数,利用题设中p、q、r的关系进一步证明.(2)先对p进行分类讨论,再对r进行分类讨论.
点评:(1)题目点明是“二次函数”,这就暗示着二次项系数p≠0,若将题中的“二次”两个字去掉,所证结论相应更改.
(2)对字母p、r分类时先对哪个分类是有一定讲究的.本题的证明中,先对p分类,然后对r分类显然是比较好的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目