题目内容
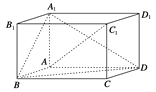
【题目】如图所示的几何体是由以等边三角形![]() 为底面的棱柱被平面
为底面的棱柱被平面![]() 所截而得,已知
所截而得,已知![]() 平面
平面![]()
![]()
![]()
![]() 为
为![]() 的中点,
的中点, ![]() 面
面![]() .
.
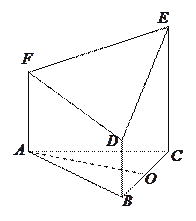
(1)求![]() 的长;
的长;
(2)求证:面![]() 面
面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 相交所成锐角二面角的余弦值.
相交所成锐角二面角的余弦值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() 为梯形
为梯形![]() 的中位线,
的中位线, ![]() ,先证明四边形
,先证明四边形![]() 为平行四边形,
为平行四边形, ![]() ,可得
,可得![]() ;(2)由平面
;(2)由平面![]() 面
面![]() ,结合
,结合![]() 可得
可得![]() 面
面![]() ,因为
,因为![]() ,所以
,所以![]() 面
面![]() ,从而得面
,从而得面![]() 面
面![]() ;(3) 以
;(3) 以![]() 为原点,
为原点, ![]() 所在直线分别为
所在直线分别为![]() 轴建立空间直角坐标系,分别求出平面
轴建立空间直角坐标系,分别求出平面![]() 与平面
与平面![]() 的一个法向量,利用空间向量夹角余弦公式可得结果.
的一个法向量,利用空间向量夹角余弦公式可得结果.
试题解析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() 为梯形
为梯形![]() 的中位线,
的中位线, ![]()
又![]() ,所以
,所以![]()
所以![]() 四点共面,因为
四点共面,因为![]() 面
面![]() ,且面
,且面![]() 面
面![]() 所以
所以![]()
所以四边形![]() 为平行四边形,
为平行四边形, ![]() 所以
所以![]()
(2)由题意可知平面![]() 面
面![]() ;又
;又![]() 且
且![]() 平面
平面![]()
所以![]() 面
面![]() ,因为
,因为![]() 所以
所以![]() 面
面![]()
又![]() 面
面![]() , 所以面
, 所以面![]() 面
面![]() ;.
;.
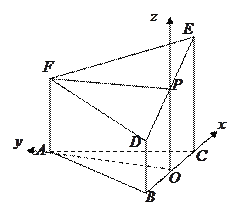
(3)以![]() 为原点,
为原点, ![]() 所在直线分别为
所在直线分别为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() 设
设![]() 为
为![]() 的中点,则
的中点,则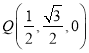 ,易证:
,易证: ![]() 平面
平面![]()
平面![]() 的法向量为
的法向量为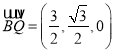
设平面![]() 的法向量为
的法向量为![]() ,
, ![]()
由![]() 得
得![]() 所以
所以![]()
所以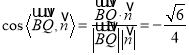 ,由所求二面角为锐二面角角,所以平面
,由所求二面角为锐二面角角,所以平面![]() 与平面
与平面![]() 相交所成锐角二面角的余弦值
相交所成锐角二面角的余弦值![]() .
.
【方法点晴】本题主要考面面垂直的证明、线面平行的定断与性质以及利用空间向量求二面角,属于难题. 空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.

【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)请将上表数据补充完整,并直接写出函数f(x)的解析式;
(2)将y=f(x)图象上所有点向左平移θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为(![]() ,0),求θ的最小值.
,0),求θ的最小值.
(3)若![]() ,求
,求![]() 的值.
的值.