题目内容
设 是△
是△ 内一点,且
内一点,且 ,
, ,定义
,定义 ,其中
,其中 、
、 、
、 分别是△
分别是△ 、△
、△ 、△
、△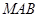 的面积,若
的面积,若 , 则
, 则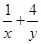 的最小值是( )
的最小值是( )
A.8 B.9 C. 16 D.18
【答案】
D
【解析】
试题分析:因为 ,
, ,所以
,所以 ,
,
所以 ,因为
,因为 ,所以
,所以
所以 即
即 的最小值为
的最小值为
考点:本小题主要考查向量的数量积运算、三角形面积公式的应用和利用“1”的整体代换和基本不等式求最值,考查了学生综合运算所学知识解决问题的能力和逻辑思维能力和运算求解能力.
点评:求解本题的关键是根据题意得出 ,然后利用“1”的整体代换和基本不等式求最值,“1”的整体代换可以简化计算,这种方法经常用到,要多加注意,多多练习.
,然后利用“1”的整体代换和基本不等式求最值,“1”的整体代换可以简化计算,这种方法经常用到,要多加注意,多多练习.

练习册系列答案
相关题目
设M是△ABC内一点,且△ABC的面积为1,定义f(M)=(m,n,p),其中m、n、p分别是△MBC,△MCA,△MAB的面积,若f(M)=(
,x,y),则
+
的最小值是( )
| 1 |
| 2 |
| 1 |
| x |
| 4 |
| y |
| A、8 | B、9 | C、16 | D、18 |