题目内容
【题目】已知元素为实数的集合![]() 满足下列条件:①
满足下列条件:①![]() ,
, ![]() ;②若
;②若![]() ,则
,则![]() .
.
(I)若![]() ,求使元素个数最少的集合
,求使元素个数最少的集合![]() ;
;
(II)若非空集合![]() 为有限集,则你对集合
为有限集,则你对集合![]() 的元素个数有何猜测?并请证明你的猜测正确.
的元素个数有何猜测?并请证明你的猜测正确.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 的元素个数为
的元素个数为![]() 的倍数;证明见解析
的倍数;证明见解析
【解析】试题分析:(Ⅰ)将![]() 分别代入②可得
分别代入②可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,再将
,再将![]() 分别代入②可得
分别代入②可得![]() ;
; ![]() ,故所求
,故所求![]() 为
为![]() . (Ⅱ)设
. (Ⅱ)设![]()
![]() 代入②有
代入②有![]() ,
, 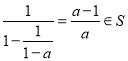 ,
, 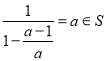 ,反证法证明
,反证法证明![]() ,
, ![]() ,
, ![]() 两两不同,
两两不同, ![]() ,;再设
,;再设 ![]() ,同理得
,同理得![]() ;所以
;所以![]() 的元素个数为
的元素个数为![]() 的倍数.
的倍数.
试题解析:
解:(I)![]() ,则
,则![]() ,
, ![]() ,可得
,可得![]() ;
; ![]() ,则
,则![]() ,
, ![]() ,可得
,可得![]() ,
,
∴![]() ,使元素个数最少的集合
,使元素个数最少的集合![]() 为
为![]() .
.
(II)非空有限集![]() 的元素个数是
的元素个数是![]() 的倍数.
的倍数.
证明如下:
(![]() )设
)设![]() 则
则![]() ,
, ![]() 且
且![]() ,则
,则![]() ,
, 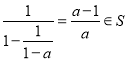 ,
, 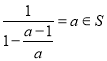
假设![]() ,则
,则![]() 无实数根,故
无实数根,故![]() .
.
同理可证![]() ,
, ![]() ,
, ![]() 两两不同.
两两不同.
即若有![]() ,则必有
,则必有![]() .
.
(![]() )若存在
)若存在![]() ,必有
,必有
![]() .
. ![]() .
.
于是![]() .
.
上述推理还可继续,由于![]() 为有限集,故上述推理有限步可中止,
为有限集,故上述推理有限步可中止,
∴![]() 的元素个数为
的元素个数为![]() 的倍数.
的倍数.

练习册系列答案
相关题目

