题目内容
如图所示,已知三棱柱ABC—A1B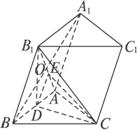
(1)求证:AB⊥CB1;
(2)求三棱柱ABC—A1B
(3)求二面角CAB1B的大小.
解析:(1)利用面面垂直的性质添加辅助线B1D,使B1D⊥AB于D;(2)求出柱体的底面积和高;(3)作出二面角的平面角.
(1)证明:在平面ABB

连结AB1.∵侧面ABB
∴B1D⊥平面ABC.
∴∠B1BA是B1B与底面ABC所成的角.
∴∠B1BA=60°.∵三棱柱的各棱长均是2,
∴△ABB1是正三角形.∴D是AB的中点.
连结CD,在正△ABC中,CD⊥AB,
∴AB⊥面B1DC.
∴AB⊥CB1.
(2)解:∵B1D⊥平面ABC,
∴B1D是三棱柱A1B
∴由B1B=2,∠B1BA=60°,得B1D=2sin60°=![]() .
.
∴三棱柱ABC—A1B![]() ×
×![]() ×2×2)
×2×2)![]() =3.
=3.
(3)解:∵△ABC为正三角形,CD⊥AB,CD⊥B1D,
∴CD⊥平面ABB1.
在平面ABB1中作DE⊥AB1于E,
连结CE,则CE⊥AB1,∴∠CED为二面角CAB1B的平面角.
在Rt△CED中,CD=2sin60°=![]() ,
,
连结BA1交AB1于O,则BO=![]() ,
,
∴DE=![]() BO=
BO=![]() .
.
∴tan∠CED=![]() =2.
=2.
∴所求二面角C-AB1-B的大小为arctan2.
小结:(1)无论在什么样的几何体中,只要有面面垂直就要考虑面面垂直的性质.(2)作出二面角的平面角并证明所作的角是二面角的平面角,然后通过解三角形求出二面角的平面角,这是求二面角的基本步骤.

练习册系列答案
相关题目
 如图所示,已知三棱柱ABC-A1B1C1的各棱长均为2,侧棱B1B与底面ABC所成的角为,且侧面ABB1A1垂直于底面ABC.
如图所示,已知三棱柱ABC-A1B1C1的各棱长均为2,侧棱B1B与底面ABC所成的角为,且侧面ABB1A1垂直于底面ABC. 如图所示,已知三棱柱A′B′C′-ABC的侧棱垂直于底面,AC⊥CB,且AC=CB=CC′=2.若点E为A′B′中点,则CE与底面ABC所成角的余弦值为
如图所示,已知三棱柱A′B′C′-ABC的侧棱垂直于底面,AC⊥CB,且AC=CB=CC′=2.若点E为A′B′中点,则CE与底面ABC所成角的余弦值为 如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为( )
如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为( ) 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 上的
上的 的中点,则异面直线
的中点,则异面直线 与
与 所成的角的余弦值为( )
所成的角的余弦值为( ) B.
B.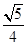 C.
C. D.
D.

 ,在某个空间直角坐标系中,
,在某个空间直角坐标系中, ,
, ,其中
,其中 、
、

 ,求直线
,求直线 与平面
与平面 所成角的大小。
所成角的大小。